naszkicuj wykres funkcji, pmocy:( tomek: Naszkicuj wykres funkcji:

	−3x+7
f(x)=		, obliczając miejsce przecięcia wykresu funkcji z osiami współrzędnych.
	x−2

Będe bardzo wdzieczny za pomoc

tomek: Naprawde nikt nie wie?

Bogdan: Dobry wieczór. Trzeba przekształcić wzór funkcji homograficznej z postaci ogólnej do postaci kanonicznej, w tym celu dzielimy licznik przez mianownik: (−3x + 7) : (x − 2) = −3 3x − 6 −−−−−−− 1

	−3x + 7		1
f(x) =		⇒ f(x) =		− 3
	x − 2		x − 2

	1
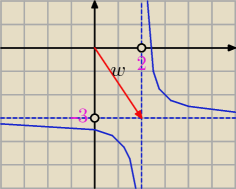
Rysujemy wykres y =		przesunięty o wektor w = [2, −3]
	x

tomek: Jejku dzięki