wielomian Radek: Mam taki wielomian W(x)=x⁴+2mx³+4x² i jest on symetryczny względem x=−1 jak wyznaczyć m ? O co chodzi z tą symetrią ?

Radek: ?

Bizon: ... da się wyciągnąć x² .... zatem 0 jest pierwiastkiem podwójnym ... Wiesz co z tego wynika?

Garth: Skoro symmetryczny wzgledem −1, to w(−2)=w(0)

Bizon:

Garth: (zakladam, ze oczwistym jest, iz wielomian o potedze parzystej jest funkcja parzysta)

Bizon: Garth ... czyżby ?

Bizon: ... jakieś nowe prawa odkrywasz −

wredulus: Skoro wielomian 4stopnia jest parzysty wzgledem prostej x=−1 to x(wierzcholka) = −1

Garth: No tak, nie jest − pospieszylem sie Kontrprzyklad wlasnie mamy wyzej.

wredulus: Skro wielomian parzystego stopnia jest symetryczny wzgledem x=−1 to w(wierzcholka) =−1

Bizon: Radek ... to do matury czy studia ?

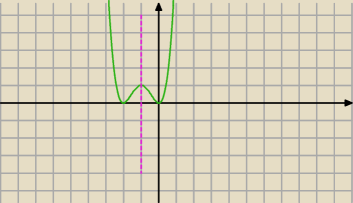
pigor: ..., a to nie jest tak, że faktycznie gdy w(−2)= w(0₌0 , czyli (−2)⁴+2m*(−2)³+4*(−2)²= 0 ⇔ 16−16m+16= 0 ⇔ m=2 , a więc w(x)= x⁴+4x³+4x²= x²(x²+2x+4)= x²(x+2)²= (x(x+2))² i wszystko się zgadza... z wykresem powyżej . ...

Radek: Przepraszam, że nie odpowiadałem ale miałem problem z internetem, poziom lo.

Radek: Dalej nie wiem o co chodzi z tą symetrią ?

Garth: Mamy funkcje o najwyzszej potedze parzystej. Jest wiec ona "parzysta" wzgledem pewnej prostej, a skoro tak, to f(x)=f(−x). Wystarczy wziac przykladowo f(−2)=f(0), rozwiazac i mamy naszem.

Garth: Znowu jakies herezje napisalem

Bizon: ... do przeczytania to https://matematykaszkolna.pl/strona/142.html Jak już przestudiujesz ... to: x=0 jest pierwiastkiem podwójnym ... czyli "odbija" x=−1 jest osią symetrii zatem drugim pierwiastkiem podwójnym musi być x=−2 ... dalej chyba rozumiesz −

Garth: Tutaj mamy raczej: f(x−1)=f(−x−1)

Maslanek: Ja to bym proponował jeszcze inaczej z tłumaczeniem f(x)=x⁴+2mx³+4x²=x²(x²+2mx+4) Stąd bezpośrednio widac, że jednym z pierwiastków jest x=0. Skoro wykres ten funkcji jest symetryczny względem prostej x=−1, to rzeczywiście f(−2)=f(0)=0 → warunek symetryczności

Mila: O to Ci chodzi Radku? Mam taki wielomian W(x)=x⁴+2mx³+4x² i jest on symetryczny względem x=−1 jak wyznaczyć m ?

Radek: Tak o to.

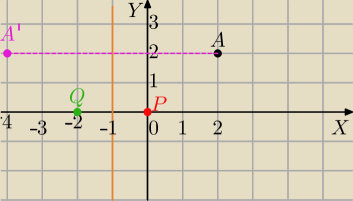
Mila: Punkt A' jest symetryczny do punktu A względem prostej x=−1. W zadaniu mamy: W(x)=x⁴+2mx³+4x² x⁴+2mx³+4x²=0⇔ x²*(x²+mx+4)=0 x=0 to w(0)=0 czyli punkt (0,0) należy do wykresu tego wielomianu, z tej zależności nie obliczymy m, musimy znaleźć inny punkt. Punktem symetrycznym do P(0,0) względem prostej x=−1 jest punkt Q(−2,0) i punkt ten należy do wykresu wielomianu⇔ w(−2)=0⇔(−2)⁴+2*m*(−2)³+4*(−2)²=0⇔ 16−16m+16=0 −16m=−32 m=2

Radek: Dziękuję już rozumiem Jeszcze proszę o pomoc w kilku zadaniach, bo chce nadrobić zaległości a mam ferie

Saizou : Wlkp?

Radek: Tak.

Saizou : ja też

Radek: To fajnie. Liczę na pomoc z w okresie ferii

Mila: Cieszę się.

Radek: Jak Pani mi tłumaczy to zawsze nie zrozumiałem staję się jasne

Mila: Empatia.

Radek: Wykaż, że jeżeli c < 0 , to trójmian kwadratowy y= x²+bx+c ma dwa różne miejsca zerowe parabola uśmiechnięta, i punkt przecięcia z osią oy jest w ujemnej ćwiartce b²−4ac b²+4c ?

kika: Nie ma pojęcia ujemna ćwiartka aΔ=b²−4ac i przy c<0 Δjest>0 stąd 2 pierwiastki.

Marcin: Fajnie że macie ferie, mi się właśnie skończyły

Mila: Δ=b²−4*1*c⇔ Δ=b²−4c>0 bo jeśli podstawisz za c liczbę ujemną to masz wynik dodatni. np. b=4, c=−8 Δ=4²−4*1*(−8)=16+32>0⇔trójmian ma dwa różne miejsca zerowe.

Radek: No tak, ale skoro mam c<0 to wzór nie powinien wyglądać tak b²+4c?

kika: Przecież Mila Tobie objaśniła , czytaj ze zrozumieniem!

zawodus: coś do kwadratu dodać liczba dodatnia = liczba dodatnia. Z tego wynikają dwa miejsca zerowe.