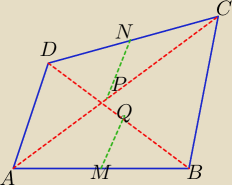
Dany jest czworokąt wypukły ABCD niebędący równoległobokiem. Punkty M, N są odpowiednio
środkami boków AB i CD. Punkty P, Q są odpowiednio środkami przekątnych AC i BD. Uzasadnij że
MQ II PN.
Korzystam z twierdzenia:
W każdym trójkącie odcinek łączący środki dwóch boków jest równoległy do trzeciego boku oraz
jest równy połowie długości trzeciego boku.
ΔADB
| AD | ||
IMΩI − to odcinek łączący środki dwóch boków IABI i IDBI , IMQI= | oraz IMQI II IADI | |
| 2 |
| AD | ||
INPI − odcinek łączący środki dwóch boków IDCI i IACI, INPI= | oraz INPI II IADI | |
| 2 |
. Dziękówka za sprawdzenie 