Nierówność wymierna asdf: Witam, pisałem dzisiaj kartk. i natrafiłem na taką nierówność.Teraz mam pytanko odnośnie ostatniej linijki, postanowiłem wyrażenie z licznika (2−x)² skrócić z tym w mianowniku, niestety Pani profesor nie zaliczyła mi zadania, z tego względu, że nie mam pojęcia co robię i tego się nie da skrócić. Nie mam już siły dopatrywania się co jest źle, prosiłbym o jakieś wsparcie. Oczywiście nie pisałem do końca, bo chce wiedzieć co jest nie tak. D:R\{2}

1
	−1>x
2−x

1
	−x−1>0
2−x

1		(x+1)(2−x)
	−		>0 /(2−x)2
2−x		2−x

1−(x+1)(2−x)*(2−x)2
	>0
(2−x)

1−(x+1)(2−x)(2−x)>0

sushi_ gg6397228: nawaliles na pałe do licznika, bez zrobienia nawiasow oraz nie skasowales mianownika

ICSP: Sprowadzenie do wspólnego mianownika :

1 − (x+1)(2−x)
	> 0 //(2−x)2
2−x

(2−x)² * [1 − (x+1)(2−x)] > 0 Teraz zajmij się tym co znajduje się w nawiasie.

wredulus_pospolitus: ja się mu nie dziwię w końcu zrobiłeś:

a − b*c
	= a − c ... interesujące
b

sushi_ gg6397228:

a		c*d
	−		>0 \ * b2
b		b

(a − c*d)*(b) >0 choc lepiej byłoby najpierw zrobi wspolny mianownik, poskracac, potem pomnozyc przez mianownik do kwadratu

asdf: Dostałem coś takiego:

(2−x2*(x2−x−1)
	>0
2−x

asdf:

(2−x)2(x2−x−1)
	>0
2−x

poprawione

wredulus_pospolitus: zacznijmy od tego ... czemu nie mogłeś tego zrobić:

1
	> x+1 //*(2−x)2
2−x

(2−x) > (x+1)(2−x)²

sushi_ gg6397228: zrób wspolny mianownik dla 3−ciej linijki w swoim pierwszym poście, nic nie usuwaj z mianownika

asdf: Czyli to co napisałem jest źle ?

asdf: up

asdf: up

wredulus_pospolitus: jak najbardziej ... 22:36 jest źle

asdf: Chyba tym sposobem co ja robiłem się po prostu nie da tego zrobić, ja nie umiem

1
	>x+1//(2−x)2
2−x

(2−x)>(x+1)(4−2x+x²)

asdf: up

asdf: up

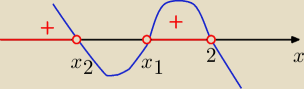
Eta: Proponuję takie rozwiązanie x≠2

1
	−1−x>0 teraz do wspólnego mianownika
2−x

1−1(2−x)−x(2−x)
	>0
2−x

1−2+x−2x+x2
	>0
2−x

x2−x−1
	>0
2−x

i do równoważnej postaci iloczynowej (2−x)(x²−x−1)>0 Δ=.... x₁= ... v x₂=... miejsca zerowe i "fala" od dołu po prawej stronie dokończ ......

asdf: Dziękuje Ci Eto za rozwiązanie, teraz tylko nie rozumiem przejścia z pierwszej linijki do drugiej

asdf: Byłbym wdzięczny gdybyś mogła to rozpisać.

Eta: Sprowadzasz do wspólnego mianownika wszystkie składniki po lewej stronie

Eta: −1 rozszerzasz o mianownik (2−x) i −x też rozszerzasz o (2−x)

1 −1*(2−x) −x*(2−x)
	>0
2−x

asdf: Ok, dzięki już rozumiem.

asdf: Hmm a dlaczego np nie tak:

1		(x+1)(2−x)
	−		>0
2−x		2−x

Eta: To jest to samo

asdf: Dziękuje Ci wytłumaczenie