RÓWNANIA KWADRATOWE, LICEUM
Unstoppable: Witam, mam problemy z paroma zadaniami, proszę o wskazówki, rozwiązanie, naprowadzenie, o
jakąkolwiek pomoc. Mam trudną sytuację rodzinną, nie potrafię się skupić, z góry dziękuję i
proszę o wyrozumiałość
Zad 1. − gdzie zrobiłem błąd?
Podana jest taka funkcja: f(x)=|x
2−2x|−x
2 Trzeba narysować wykres tej funkcji
Rozpisałem to mniej więcej w ten sposób:
f(x)=|x(x−2)|−x
2
x(x−2) ≥0 <=> x∊<0,2>
x(x−2) <0 <=> x∊(−
∞,0) U (2,+
∞) (U − suma)
Na koniec wyszło coś takiego:
f(x)=
| ⎧ | −2x, jeśli x∊<0,2> | |
| ⎩ | −2x2+2x, jeśli x∊(−∞,0) U (2,+∞) |
|
A w odpowiedziach pisze, że:
f(x)=
| ⎧ | −2x, jeśli x∊(−∞,0) U (2,+∞) | |
| ⎩ | −2x2+2x, jeśli x∊<0,2> |
|
Czyli na odwrót, co jest nie tak? Aha i jak narysować wykres funkcji y=−2x
2+2x?
| | 1 | | 1 | |
Czy poprzez translację wykresu y=−2x2 o wektor( |
| , |
| )? |
| | 2 | | 2 | |
Zad 2.
Jest funkcja f(x)= |x
2−2x|−3 − jak narysować wykres tej funkcji stosując odpowiednie
przekształcenia? (Dobrze zacząłem to zadanie?)
f(x)= |x
2−2x|−3
x(x−2)≥0 <=> x∊<0,2>
x(x−2)<0 <=> x∊(−
∞,0) U (2,+
∞)
(co dalej?)
Zad 3.
Z tym zadaniem nie wiem co zrobić treść tego zadania brzmi: "Naszkicuj wykres funkcji
f(x)=|x
2−4|+|x
2−x|, x∊R
a) Podaj wzór funkcji, nie używając znaku wartości bezwzględnej.
b) Na podstawie wykresu funkcji określ:
− Zbiór wartości tej funkcji
− Liczbę rozwiązań równania f(x)=4
− Zbiór rozwiązań nierówności f(x)>−x+4
Zad 4.
Treść brzmi następująco: Zbadaj liczbę rozwiązań równanie ze względu na wartość parametru m
(m∊R) (dobrze zrobiłem?)
kanoniczna postać
to: y=a(x+p)
2+q
więc:
b=3
Δ= −2 (z wzoru b
2−4ac)
p= −3
q= 1
więc teraz przekształcenia
| | 1 | | 1 | |
y= |
| x2 →[−3,1] (Translacja o wektor) y= |
| (x+3)2+1 → (symetria o oś OX) |
| | 2 | | 2 | |
| | 1 | | 1 | |
f(x)= | |
| x2 + 3x + 5 |
| | |
| | 2 | | 2 | |
Jak to narysować i przyrównać do m?
Zad 5.
Zadanie podobne tylko, że gdzie indziej wartość bezwzględna i to mnie totalnie zmyliło...
| | 1 | | 1 | |
− |
| x2 − |
| |x| + 3 = m |
| | 2 | | 2 | |
31 sty 21:29
sushi_ gg6397228:
zad1. załozenia odwrotnie
x(x−2) ≤0 dla 0≤x≤2
31 sty 21:33
wredulus_pospolitus:
1)
x*(x−2) < 0 gdy x∊(0,2) ... ponieważ jest to parabola z ramionami skierowanymi do góry ...
więc wartość funkcji dla zbioru pomiędzy miejscami zerowymi będzie zbiorem liczb ujemnych
31 sty 21:33
wredulus_pospolitus:
f(x) = −2x2+2x = −2x*(x−1) <−−− parabola, ramiona do dołu ... miejsca zerowe 0 i 1 ... a
więc ... tak
31 sty 21:36
Unstoppable: Jeszcze raz proszę o pomoc. Jestem zmęczony po całym dniu opieki nad chorą siostrą, rano
wstanę, przeczytam i wezmę się do roboty. Niestety mam więcej jeszcze zadań do zrobienia, ktoś
mógłby mi pomóc na weekendzie? Chociaż naprowadzić albo poprawić błędy. Kontakt do mnie gg:
2885078, skype: Unstoppable, e−mail: feniks12@vp.pl. Dziękuję bardzo

31 sty 21:36
wredulus_pospolitus:
zad 2 ... ten sam błąd co w zadaniu 1

31 sty 21:36
Mila:
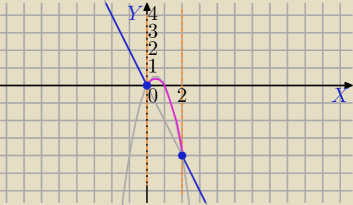
1)
Podana jest taka funkcja: f(x)=|x
2−2x|−x
2
a) |x
2−2x|=x
2−2x⇔x
2−2x≥0 ⇔x(x−2)≥0⇔x≤0 lub x≥2 ( parabola skierowana do góry)
wtedy masz wzór f(x) taki:
f(x)=x
2−2x−x
2⇔
f(x)=−2x dla x≤0 lub x≥2
b)| x
2−2x|=−x
2+2x dla x
2−2x<0 ⇔x∊(0,2)
wtedy f(x) ma wzór:
f(x)=−x
2+2x−x
2⇔f(x)=−2x
2+2x
f(x)=−2x2+2x dla x∊(0,2)
31 sty 21:52
Mila:
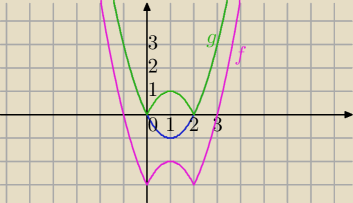
Zadanie 2)Jest funkcja f(x)= |x
2−2x|−3 − jak narysować wykres tej funkcji stosując odpowiednie
przekształcenia? (Dobrze zacząłem to zadanie?)
1) rysujesz wykres funkcji (szkic)
y=x2−2x
x
2−2x=0
x=0 lub x=2 miejsca zerowe
y
w=1
2−2*1=1−2=−1
(1,−1) wsp. wierzchołka paraboli
2)
y=x2−2x→S
Ox dla y<0 →
g(x)=|x2−2x|
(odbicie do góry , tej części wykresu, która leży pod osią OX)
3)
g(x)=|x2−2x|→T
[0,−3]→
f(x)= |x2−2x|−3
(translacja o wektor [0,−3])
31 sty 22:10
Mila:
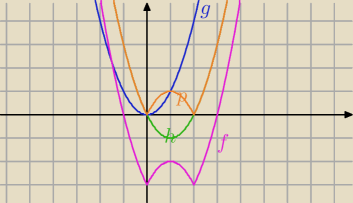
zadanie 2 inaczej
Jest funkcja f(x)= |x
2−2x|−3 narysować wykres tej funkcji stosując odpowiednie
przekształcenia.
g(x)=x
2−2x
x
w=1
y
w=−1
f(x)=|(x−1)
2−1|−3
1)
g(x)=x2→T
[1,−1]→
h(x)=(x−1)2−1→S
OX dla y<0 →
p(x)=|x2−2x|→
→T
[0,−3]→
f(x)= |x2−2x|−3
31 sty 22:47
Mila:
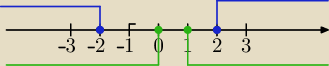
zadanie 3)
Naszkicuj wykres funkcji
f(x)=|x
2−4|+|x
2−x|, x∊R
|x
2−4|=x
2−4 ⇔(x−2)*(x+2)≥0⇔x≤−2 lub x≥2
|x
2−x|=x
2−x ⇔x(x−1)≥0 ⇔x≤0 lub x≥1
Zaznaczę na osi przedziały, a wykres będzie w natępnym wpisie:
Ustalamy wzory funkcji w przedziałach:
a) (−
∞,−2)U(2,
∞)
f(x)=x
2−4−(x
2−x)=x
2−4−x
2+x
f(x)=x−4 dla x∊ (−∞,−2)U(2,∞)
b) x∊(−2,0>U<1,2)
f(x)=−x
2+4−(x
2−x)=−x
2+4−x
2+x
f(x)=−2x2+x+4 dla x∊(−2,0>U<1,2)
c) x∊(0,1)
f(x)=−x
2+4−(−x
2+x)
f(x)=−x+4 dla x∊(0,1)
31 sty 23:17
Mila:
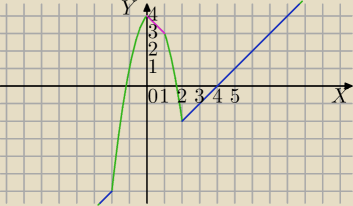
zadanie 3) cd.
f(x)=|x
2−4|−|x
2−x|
Z
w=(−
∞,
∞)
31 sty 23:24
Mila:

zadanie 3) cd.
f(x)=|x
2−4|−|x
2−x|
y=4
f(x)=4⇔x=0 lub x=8
Zbiór rozwiązań nierówności f(x)>−x+4⇔
wykres f(x) leży nad wykresem funkcji y=−x+4 dla x>4
31 sty 23:31
Unstoppable: Mila, stokrotne dzięki

1 lut 10:02
Mila:
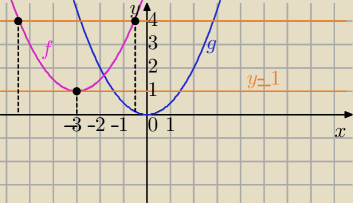
zadanie 4 .
Rysujesz wykres tak jak, napisałeś.
| | 1 | | 1 | |
g(x)= |
| x2→T[−3,1]→h(x)=f(x)=| |
| (x+3)x2+1| |
| | 2 | | 2 | |
| | 1 | | 1 | |
Δ<0 i a>0 to funkcja y= |
| x2+3x+5 |
| przyjmuje tylko wartości dodatnie |
| | 2 | | 2 | |
x
w=−3
y
w=1
Równanie:
f(x)=m
y=m
1) dla m<1 brak rozwiązań (prosta y=m nie przecina wykresu parboli)
2) dla m=1⇔jedno rozwiązanie
3)m>1 dwa rozwiązania.
1 lut 12:10
Mila:
Zadanie 5 później.
1 lut 12:10
Mila:
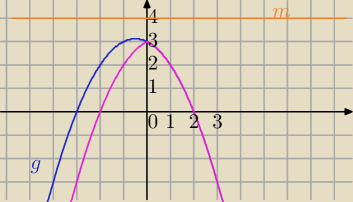
Zadanie 5)
1) rysujesz wykres funkcji;
x
1=2 lub x
2=−3
Szkicujesz wykres g(x)
Potem interesuje Cię tylko część wykresy z prawej strony OY i ją odbijasz względem OY.
| | −1 | | 1 | | −1 | | 1 | |
g(x)= |
| x2− |
| x+3→SOY dla x≥0)→f(x)= |
| x2− |
| |x|+3 |
| | 2 | | 2 | | 2 | | 2 | |
2) równanie f(x)=m
dla m>3 brak rozwiązań
dla m=3 jedno rozwiązanie
dla m<3 dwa rozwiązania
1 lut 21:36


 1)
Podana jest taka funkcja: f(x)=|x2−2x|−x2
a) |x2−2x|=x2−2x⇔x2−2x≥0 ⇔x(x−2)≥0⇔x≤0 lub x≥2 ( parabola skierowana do góry)
wtedy masz wzór f(x) taki:
f(x)=x2−2x−x2⇔f(x)=−2x dla x≤0 lub x≥2
b)| x2−2x|=−x2+2x dla x2−2x<0 ⇔x∊(0,2)
wtedy f(x) ma wzór:
f(x)=−x2+2x−x2⇔f(x)=−2x2+2x
f(x)=−2x2+2x dla x∊(0,2)
1)
Podana jest taka funkcja: f(x)=|x2−2x|−x2
a) |x2−2x|=x2−2x⇔x2−2x≥0 ⇔x(x−2)≥0⇔x≤0 lub x≥2 ( parabola skierowana do góry)
wtedy masz wzór f(x) taki:
f(x)=x2−2x−x2⇔f(x)=−2x dla x≤0 lub x≥2
b)| x2−2x|=−x2+2x dla x2−2x<0 ⇔x∊(0,2)
wtedy f(x) ma wzór:
f(x)=−x2+2x−x2⇔f(x)=−2x2+2x
f(x)=−2x2+2x dla x∊(0,2)
 Zadanie 2)Jest funkcja f(x)= |x2−2x|−3 − jak narysować wykres tej funkcji stosując odpowiednie
przekształcenia? (Dobrze zacząłem to zadanie?)
1) rysujesz wykres funkcji (szkic)
y=x2−2x
x2−2x=0
x=0 lub x=2 miejsca zerowe
Zadanie 2)Jest funkcja f(x)= |x2−2x|−3 − jak narysować wykres tej funkcji stosując odpowiednie
przekształcenia? (Dobrze zacząłem to zadanie?)
1) rysujesz wykres funkcji (szkic)
y=x2−2x
x2−2x=0
x=0 lub x=2 miejsca zerowe
 zadanie 2 inaczej
Jest funkcja f(x)= |x2−2x|−3 narysować wykres tej funkcji stosując odpowiednie
przekształcenia.
g(x)=x2−2x
xw=1
yw=−1
f(x)=|(x−1)2−1|−3
1) g(x)=x2→T[1,−1]→h(x)=(x−1)2−1→SOX dla y<0 →p(x)=|x2−2x|→
→T[0,−3]→ f(x)= |x2−2x|−3
zadanie 2 inaczej
Jest funkcja f(x)= |x2−2x|−3 narysować wykres tej funkcji stosując odpowiednie
przekształcenia.
g(x)=x2−2x
xw=1
yw=−1
f(x)=|(x−1)2−1|−3
1) g(x)=x2→T[1,−1]→h(x)=(x−1)2−1→SOX dla y<0 →p(x)=|x2−2x|→
→T[0,−3]→ f(x)= |x2−2x|−3
 zadanie 3)
Naszkicuj wykres funkcji
f(x)=|x2−4|+|x2−x|, x∊R
|x2−4|=x2−4 ⇔(x−2)*(x+2)≥0⇔x≤−2 lub x≥2
|x2−x|=x2−x ⇔x(x−1)≥0 ⇔x≤0 lub x≥1
Zaznaczę na osi przedziały, a wykres będzie w natępnym wpisie:
Ustalamy wzory funkcji w przedziałach:
a) (−∞,−2)U(2,∞)
f(x)=x2−4−(x2−x)=x2−4−x2+x
f(x)=x−4 dla x∊ (−∞,−2)U(2,∞)
b) x∊(−2,0>U<1,2)
f(x)=−x2+4−(x2−x)=−x2+4−x2+x
f(x)=−2x2+x+4 dla x∊(−2,0>U<1,2)
c) x∊(0,1)
f(x)=−x2+4−(−x2+x)
f(x)=−x+4 dla x∊(0,1)
zadanie 3)
Naszkicuj wykres funkcji
f(x)=|x2−4|+|x2−x|, x∊R
|x2−4|=x2−4 ⇔(x−2)*(x+2)≥0⇔x≤−2 lub x≥2
|x2−x|=x2−x ⇔x(x−1)≥0 ⇔x≤0 lub x≥1
Zaznaczę na osi przedziały, a wykres będzie w natępnym wpisie:
Ustalamy wzory funkcji w przedziałach:
a) (−∞,−2)U(2,∞)
f(x)=x2−4−(x2−x)=x2−4−x2+x
f(x)=x−4 dla x∊ (−∞,−2)U(2,∞)
b) x∊(−2,0>U<1,2)
f(x)=−x2+4−(x2−x)=−x2+4−x2+x
f(x)=−2x2+x+4 dla x∊(−2,0>U<1,2)
c) x∊(0,1)
f(x)=−x2+4−(−x2+x)
f(x)=−x+4 dla x∊(0,1)
 zadanie 3) cd.
f(x)=|x2−4|−|x2−x|
Zw=(−∞,∞)
zadanie 3) cd.
f(x)=|x2−4|−|x2−x|
Zw=(−∞,∞)
 zadanie 3) cd.
f(x)=|x2−4|−|x2−x|
y=4
f(x)=4⇔x=0 lub x=8
Zbiór rozwiązań nierówności f(x)>−x+4⇔
wykres f(x) leży nad wykresem funkcji y=−x+4 dla x>4
zadanie 3) cd.
f(x)=|x2−4|−|x2−x|
y=4
f(x)=4⇔x=0 lub x=8
Zbiór rozwiązań nierówności f(x)>−x+4⇔
wykres f(x) leży nad wykresem funkcji y=−x+4 dla x>4

 zadanie 4 .
Rysujesz wykres tak jak, napisałeś.
zadanie 4 .
Rysujesz wykres tak jak, napisałeś.
 Zadanie 5)
1) rysujesz wykres funkcji;
Zadanie 5)
1) rysujesz wykres funkcji;