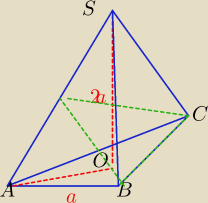
 Dany jest ostrosłup prawidłowy trójkątny o krawędzi podstawy a i wysokości 2a. Ostrosłup
przecięto płaszczyzną prostopadła do krawędzi bocznej i przechodzącą przez krawędź podstawy,
Oblicz pole otrzymanego przekroju.
Może ktoś pomóc z rysunkiem ?
Dany jest ostrosłup prawidłowy trójkątny o krawędzi podstawy a i wysokości 2a. Ostrosłup
przecięto płaszczyzną prostopadła do krawędzi bocznej i przechodzącą przez krawędź podstawy,
Oblicz pole otrzymanego przekroju.
Może ktoś pomóc z rysunkiem ?
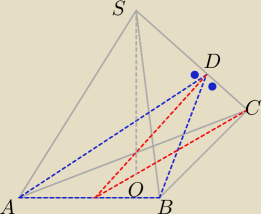

 W ostrosłupie prawidłowym trójkątnym o wysokości H i kącie nachylenia krawędzi bocznej do
płaszczyzny podstawy 2α poprawdzono płaszczyznę przez krawędź podstawy. Płaszczyzna ta jest
nachylona do płaszczyzny podstawy pod kątem α. Oblicz pole otrzymanego przekroju.
Można prosić o pomoc ? Na razie wyliczyłem bok a
W ostrosłupie prawidłowym trójkątnym o wysokości H i kącie nachylenia krawędzi bocznej do
płaszczyzny podstawy 2α poprawdzono płaszczyznę przez krawędź podstawy. Płaszczyzna ta jest
nachylona do płaszczyzny podstawy pod kątem α. Oblicz pole otrzymanego przekroju.
Można prosić o pomoc ? Na razie wyliczyłem bok a
| √3H | ||
a= | ||
| tg2α |

| a√3 | ||
b = √ 4a2 + (a2/3) = ..., h = | , | |
| 2 |
| 2a | w | |||
Z podobieństwa trójkątów: | = | ⇒ w = ... | ||
| b | h |
| 1 | ||
Pole przekroju P = | aw | |
| 2 |