p Radek: Wyznacz wszystkie wartości parametru m, dla których wartość bezwzględna różnicy pierwiastków równania 2x²+(1−2m)x−m=0 jest mniejsza od 5 Pierwszy warunek wychodzi błędnie Δ≥0 (1−2m)²+8m≥0 1−4m+4m²+8m≥0 4m²+4m+1≥0 (2m+1)²≥0 to wychodzi, że m∊{−0,5}

Marcin: Δ=0, współczynnik przy x² dodatni, także m∊R

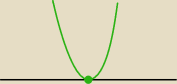
Radek: przecież dotyka oś

Saizou : z pierwszego warunku wychodzi że m∊R

Marcin: No tak, ale masz ≥ 0, także 0 też pasuje.

Radek: ?

Piotr 10: Podstaw sobie za m=−0,5 (2*(−0,5)+1)² ≥ 0 (−1+1)² ≥ 0 0 ≥ 0 co jest prawdą

Marcin: Nie bardzo wiem w czym masz problem Wszystko wydaje się jasne

Radek:

	1
no tak ale więc czemu m∊R a nie m∊{−		)
	2

Marcin: Bo jakąkolwiek liczbę byś nie wstawił za x, to zawsze będzie ona ≥0

Marcin: czy tam za m w tym przypadku.

Saizou : a jak byś rozwiązał nierówność kwadratową typu 4x²+4x+1≥0

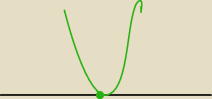
Radek: (2x+1)²≥0

	1
x=−
	2

Marcin: Sam rysujesz dobrze parabole, a później piszesz bzdury

Saizou : ale to jest nierówność a nie równanie zatem....

zawodus: klasyczny problem nie rozumienia nierówności słabej. DOWOLNA LICZBA RZECZYWISTA PODNIESIONA DO KWADRATU JEST NIEUJEMNA...

Radek:

	1
jak by było ≤o wtedy by było x=−		dzięki zapomniałem
	2

Marcin: Jakby było ≤0, to pasowałoby Ci tylko 0