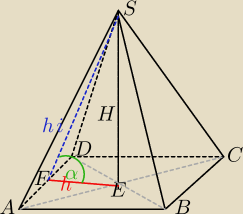
Oblicz sinus kąta :) aaagaaa: Dany jest ostrosłup prawidłowy czworokątny ABCDS o podstawie ABCD . W trójkącie równoramiennym ASC stosunek długości podstawy do długości ramienia jest równy |AC | : |AS | = 6 : 5 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy. Mogę zrobić to tak? : |AC|=6 , |AS|=5 |AC| to przeciwprostokątna kwadratu, czyli |AD|√2=6 Obliczam |AD|. |AD|=3√2 Przekątne w kwadracie się połowią, czyli |AE|=|EC|=|BE|=|ED|=3 i przecinają się pod kątem prostym. Obliczamy drugą (czerwoną) wysokość trójkąta AED. Jeżeli wiemy, że |AE|=|ED|=3 to pole trójkąta AED :

	|AE|*|DE|		3*3		9
P=		=		=		= 4,5
	2		2		2

	|AD|*h
znajdujemy wysokość czerwoną P=
	2

	3√2*h
4,5=		po przekształceniu h=1,5√2
	2

Obliczamy niebieską wysokość |AF|²+hi²=5² (1,5√2)²+hi²=25 4,5+hi²=25 hi²=20,5 hi=√20,5 Obliczamy wysokość ostrosłupa: H H²+|AE|²=|AS|² H²+3²=5² H²+9=25 H²=16 H=4

	H		4		4*√20,5
czyli sinα =		= sinα =		=
	hi		√20,5		20,5

Mam nadzieję, że niczego nie pomyliłam w przepisywaniu

wredulus_pospolitus:

	1		1
Małe ułatwienie ... h (wysokość ΔAED) =		AB =		AD (połowa długości boku
	2		2

kwadratu) to by Ci zaoszczędziło parę minut

aaagaaa: ale dobrze jest poza tym ?