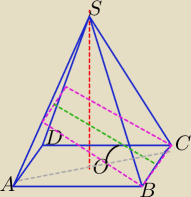
. Piotr 10: Dany jest ostrosłup prawidłowy czworokątny. Krawędź podstawy ostrosłupa ma długość a. Ściana boczna jest nachylona do płaszczyzny podstawy ostrosłupa pod kątem α. Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź podstawy i nachyloną do płaszczyzny podstawy pod kątem

	1
		α. Oblicz pole otrzymanego przekroju.
	3

Czy rysunek jest dobry ?

	1
ten kąt		α jest zawarty między wsokością trapezu a przekątna kwadratu ( taki mały ''łuk
	3

czarny)

Mila:

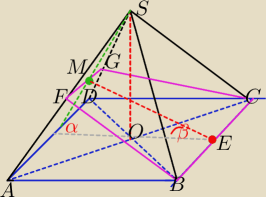
	1
β=		α
	3

Piotr 10: Ok

Piotr 10: Zrobiłem, strasznie dużo liczenia było Wynik

	sinα		sin(1/3α)sinαcosα
Pprzekroju=a2[		−		]
	sin(4/3α)		sin2(4/3α)

Zgadza się z odpowiedzią, dziękuję za rysunek