wykres z logarytmem bla bla : W układzie współrzednych zaznaczyć zbiór punktów spełniających warunki: log₂ (^{x y}₂) − log₂x * log₂y = 0 nie za bardzo wiem jak sie do tego zabrac. Na pewno x>0 i y>0

Eta: zał: x >0 i y>0 log₂x +log₂y − log₂2 − log₂x *log₂y=0 log₂x −log₂x*log₂y +log₂y −1=0 log₂x( 1 − log₂y) −( 1 −log₂y)=0 ( 1 −log₂y)( log₂x −1)=0 log₂y= 1 v log₂x =1 y= 2 v x= 2 P(2,2) −−− jedyny taki punkt , który spełnia ten warunek

bla bla : dziekuje Eta nie wpadłam na to żeby to pogrupowac

Eta: I w tym rzecz Pozdrawiam!

Bogdan: A np. punkt (4, 2) ?

Eta: No właśnie (4,2) i (2,4) wytłumacz mi Bogdanie , czemu przy rozkładzie na czynniki nie wyszły mi te punkty? bo juz teraz nie myślę

Bogdan: a punkt np. B = (2, 19) ?

Bogdan: albo C = (2, π) ?

Eta: Ok Powiedz jak ma wygladać rozwiązanie bo chcę spokojnie zasnąć

Eta: Wrrrrrrrrrr

AROB: Też jestem ciekawa, skąd wziął Bogdan te punkty.

Bogdan: Zaraz pokażę rozwiązanie

Eta: No nie wiem za diabła co "skopałam"

Bogdan: Ale te punkty spełniają równość, prawda ?

Eta: Zastanawiałam się ,że w zad. było polecenie" wyznacz zbiór punktów" ! i nijak mi nie wychodziły

Eta: Bogdan nie drażnij sie ze mną i dawaj rozwiązanie ,bo zawał mi grozi a jeszcze chcę pożyć

Bogdan: Już piszę, moment

Eta: ok

AROB: Też czekam. A chcę iść już .

Bogdan:

	xy
log2		− log2 x * log2 y = 0, x > 0, y > 0.
	2

	xy
log2		= log2 y * log2 x
	2

xy
	= y * log2 x / :y to y∊(0, +∞)
2

x
	= log2 x ⇒ x = 2 lub x = 4
2

Odp.: Rozwiązaniem jest zbiór punktów (2, y∊(0,+∞)) oraz oddzielny punkt (4, 2)

	1
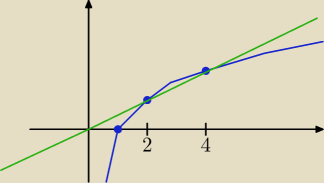
Rysunek przedstawia wykresy funkcji y =		x oraz y = log2 x
	2

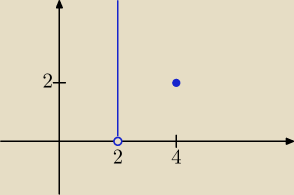
Bogdan: To jest rozwiązanie

Bogdan: Jest coś tu do poprawienia

Bogdan: Proszę sprawdzić dowolny punkt (2, y) dla y∊(0, +∞)

Eta: Ot to Dzięki za wyjasnienie. Dobranoc, AROB i Bogdanie

Eta: Jak widać ( urodziłam się "głupia" i chyba "głupia" umrę

AROB: A ja nie rozumiem, jak przeszedłeś z II linii pod wykresem do III linii. Ja widzę tam mnożenie 2 logarytmów, a nie log₂(y*log₂x). Odpowiedz, jeśli możesz jeszcze , na dobranoc.

Bogdan: W moim rozwiązaniu jest nieścisłość, gdzie?

AROB: No ja właśnie nie widzę możliwości opuszczenia znaków logarytmów.

Bogdan: AROB dostrzegła. A odpowiedź jest poprawna?, czy każdy z punktów prostej x = 2 dla y > 0 spełnia to równanie?

Bogdan: a także punkt (4, 2)?

Eta: Już teraz to wyłączył mi się mózg

Eta: Miłych snów

AROB: Rzeczywiście punkty (2,1) i (4,2) spełniają równanie. I to chyba wszystko. Tylko dlaczego rachunkowo trudno to otrzymać?

Bogdan: Przepraszam za zamieszanie, dobranoc

AROB: Już zmykam spać, bo kto za mnie jutro wstanie? , Dobranoc Wam! Do jutra.

Bogdan: AROB, a inne punkty prostej x = 2 dla y > 0 tez spełniają równanie ?

Eta: ( 2,π) L=log₂2 +log₂π−log₂2 = log₂π P=log₂2*log₂π= log₂π L=P czemu nie otrzymamy tego rozwiazania po rozkładzie na czynniki..... to tego już nie wiem?

Bogdan: (2, y) dla y > 0

	2y
log2		= log2 y * log2 2
	2

log₂ y = log₂ y

Eta: A co z takimi punktami? (x,2) dla x>0 mamy podobnie:

	2x
log2		= log2x*log22
	2

log₂x = log₂x

Eta: I teraz już wiem czemy z rozkładu wyszedł mi punkt(2,2) Czy tak?

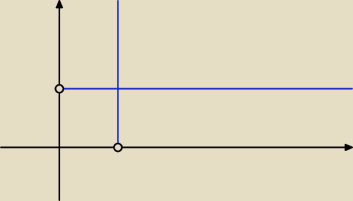
Bogdan: Jest jeszcze więcej rozwiązań. Kolejnym zbiorem są wszystkie punkty prostej y = 2 dla x > 0

Eta: byłam szybsza

Bogdan: teraz musimy do tego dojść

Eta: No to teraz Nasza bla bla ma pełny obraz , co robią matematycy w środku nocy gdy Ona smacznie Idziemy już i my do Doranoc

Bogdan: Jeszcze moment, poczekajcie, podaję odpowiedź

Eta: ok Namieszałeś , to "odmieszaj"

Bogdan: Eto, Twoje rozwiązanie: log₂ y = 1 v log₂ x = 1 jest jak najbardziej prawidłowe, tylko niedokładnie zinterpretowane. Jeśli log₂ y = 1 v log₂ x = 1, to y = 2 lub x = 2, ale nie y = 2 i x = 2. Wzięcie y = 2 i x = 2 daje punkt (2, 2), ale tu mamy sumę zbiorów, a nie iloczyn. Mamy więc prostą y = 2 oraz prostą x = 2 dla y > 0, x > 0

Eta: Wrrrrrrrrr wszystko przez tem mały znaczek "lub" no tak Bogdan jak mogłeś mnie tak trzymać w takim napięciu Ech ...

Bogdan: no to "odmieszałem'', teraz naprawdę już dobranoc.

Eta: AROB Widzisz już jacy są "faceci" ? ....... od zawsze to wiedziałam ,że się pastwią nad płcią piękną Superr , wszystko jasne ....teraz mogę spokojnie iść do Dobranoc!

Bogdan: Ja tylko chciałem spędzić z Wami trochę nocy

Eta: OK Miło było, ale mogłam tego nie przeźyć Do jutra

Bogdan: Sytuacja była pod kontrolą

Eta: Ach Bogdanie z Ciebie Dobranoc!

AROB: Ja Was wczoraj opuściłam, nie spodziewając się tak ciekawej dalszej dyskusji. Kosztowało mnie to tyle, że zasnąć mi ten problem nie pozwalał, a skoro świt ruszyłam z równaniem od nowa. No i doszłam do tego samego wniosku, co stwierdziliście w nocy. Rzeczywiście jest nieskończona ilość rozwiązań postaci: x=2 i y∊(0,∞) lub y=2 i x∊(0,∞). Ach, ta matematyka! I jak tu jej nie lubić! Nic nie da się pominąć. Taki jeden znaczek "∨" tyle dyskusji sprowokował. P.S. Żal mi tylko, że planowałam Wam przekazać moje "odkrycia", a tu "musztarda po obiedzie". Do wieczora, Eto i Bogdanie, pozdrawiam.

AROB: Dobry wieczór Eto i Bogdanie

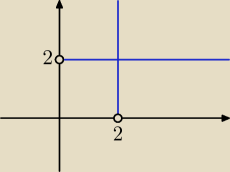
Bogdan: Dobry wieczór AROB i Eto. To nocne zadanie jest przykładem tego, jak bardzo ważne jest zwracanie uwagi na zapisy w zadaniu. Sam się naciąłem zapisując początkowo

	xy
na kartce równość w postaci log2		= log2xlog2y, co zasugerowało mi, że
	2

	xy
jest log2		= log2(xlog2y), a to w konsekwencji doprowadziło do zapisu
	2

xy		y
	= xlog2y i dalej do		= log2y.
2		2

	xy
Poprawny zapis jest natomiast taki: log2		= (log2x)(log2y) dla x > 0 i y > 0.
	2

Po przekształceniach otrzymuje się wynik podany przez Etę, to jest x = 2 ⋁ y = 2, tu kluczową rolę odgrywa znak ⋁ wskazujący na punkty leżące na prostych: x = 2 dla x > 0 oraz punkty leżące na prostej y = 2 dla y > 0.

AROB: Dzięki Bogdanie, wszystko już jest jasne.