bryły
bezendu:
Pomoże ktoś zrozumieć te bryły od podstaw ?
29 sty 22:10
bezendu:
Przekroje, trójkąty prostokątne itp ?
29 sty 22:12
bezendu: ?
29 sty 22:17
bezendu:

jeśli mam gra.pra czw to w tym trójkącie nie będzie kątów prostych ?
29 sty 22:21
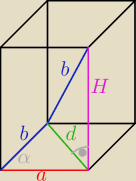
Saizou :
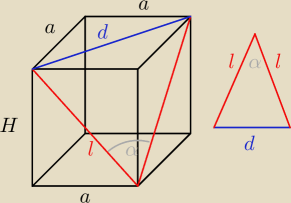
d=a
√2 jako przekątna kwadratu
l=
√a2+H2 z tw. Pitagorasa
gdyby miał być kąt prosty to α musi być tym kątem
l
2+l
2=d
2
2l
2=d
2
2
√a2+H2=(a
√2)
2
2a
2+2H
2=2a
2
H=0 co jest sprzeczne zatem nie może być tam kąta prostego
29 sty 22:30
bezendu: dziękuję !
29 sty 22:31
bezendu: A od jakich zadań mam zacząć bo na zadania.info trochę za trudne
29 sty 22:34
Lorak: Może od zadań z podręcznika?

29 sty 22:41
bezendu: w podręczniku z kolej są za proste.
29 sty 22:41
Lorak: Czyli podstawy rozumiesz

29 sty 22:44
bezendu: Ja już sam nie wiem co rozumiem i co ja tutaj robię.
29 sty 22:45
Saizou : dasz radę

łap zadanko
Jaką objętość ma czworościan foremny o krawędzi długości a
29 sty 22:48
bezendu:
29 sty 22:54
Saizou : pokaż jak obliczyłeś wysokość

29 sty 22:56
bezendu:
ze wzoru na wysokość trójkąta równobocznego

29 sty 22:57
Saizou :
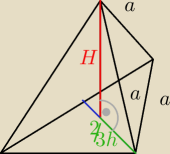
ale czy wysokość całej bryły jest równa wysokości np. podstawy ?
29 sty 23:00
bezendu:
Czyli źle mam ?
29 sty 23:01
Saizou : tak, ale policz raz jeszcze
29 sty 23:02
Mila:
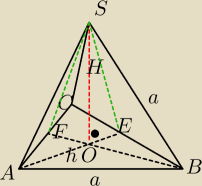
Najpierw rysunek:
29 sty 23:08
29 sty 23:08
Saizou : jaki jest wzór na wysokośc w trójkącie równobocznym ?
29 sty 23:09
bezendu:

29 sty 23:11
Saizou : 
zatem V=?
29 sty 23:11
29 sty 23:14
Saizou : | | 2 | |
ale wyliczyłeś |
| h podstawy  i teraz pitagoras aby obliczyć H jako wysokość bryły  |
| | 3 | |
29 sty 23:15
29 sty 23:25
Saizou :
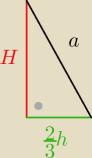
i teraz dokończ
....
V=....
29 sty 23:28
bezendu:
Nie bardzo rozumiem czemu nie mogę do policznia wysokości brać wysokości trójkąta rówobocznego
29 sty 23:33
Godzio:
To pokaż jak liczysz tą wysokość, to wskażemy błąd.
29 sty 23:35
bezendu:
| | a√3 | |
Wysokość ściany bocznej to h= |
| ? |
| | 2 | |
| | 2 | | a√3 | |
A |
| wysokości podstawy to |
| |
| | 3 | | 3 | |
| | a√3 | | a√3 | |
H=( |
| )2−U( |
| )2? tak liczę. |
| | 2 | | 3 | |
29 sty 23:50
Godzio:
| | 1 | | 2 | |
Tam jest |
| wysokości, a nie |
| |
| | 3 | | 3 | |
29 sty 23:55
bezendu:
| | 2 | |
a jeśli bym brał do |
| to zamiast wysokości ściany bocznej długość krawędzi ? |
| | 3 | |
29 sty 23:57
Godzio:
Tak
29 sty 23:58
bezendu: dzięki
29 sty 23:58
5-latek: Wiem ze nie lubisz zadan ode mnie ale ja jednak bede CI wstawial a czy skorzytasz to juzz alezy
od Ciebie>
W graniastoslupie prostym podstawa jest rownoleglobok o bokach a i b oraz o kacie ostrym alfa
.
Znalezc objetosc graniastoslupa jesli wiadomo ze mniejsza przerkatna graniastoslupa rowna sie
weikszej przekatnej podstawy .
30 sty 09:01
5-latek: zadanie nr 2.
W ostroslupie prawidlowym czworokatnym odleglosci srodka wysokosci od krawedzi bocznej i
sciany bocznej wynosza odpowiednio a i b .
Obliczyc objetosc ostroslupa i podac warunek rozwiazywalnosci zdania
Zadanie nr 3
Szescian przecieto plaszczyzna przechodzaca przez przekatna dolnej podstzwy i srodki dwoch
sasiednich krawedzi gornej podstawy .
Znalezc sinus kata miedzy przekatnymi otrzymanego przekroju .
Na tym koniec
30 sty 10:31
5-latek:
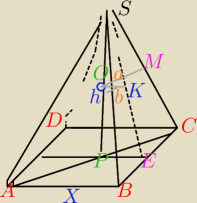
30 sty 10:45
Heniek:
a co to za bazgroły, masakra
30 sty 12:11
5-latek: Tylko ewntualnie Eta albo Mila maja prawo zwracac mi uwage za rysunki
Ty niestety kolego nie .
ja zawsze w pracy mowie . jesli chcesz zebym zrobil wiecej to pokaz jak . ja wtedy tak bede
robil .
Wiec narysuj lepiej OK?
30 sty 13:24
bezendu:
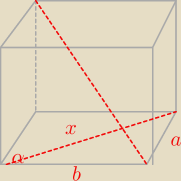
x
2=a
2+b
2−2(a*b*cos(180−α))
x
2=a
2+b
2−(2ab*(−cosα))
x
2=a
2+b
2+2abcosα
x=
√a2+b2+2abcosα
I dalej nie wiem dokończę jak wrócę ze szkoły.
30 sty 13:36
bezendu:
Nie bardzo wiem jak zrobić te zadania, a jak ktoś mi rozwiążę to w życiu nie nauczę się tego,
więc to chyba jednak traci sens.
30 sty 16:33
Mila:
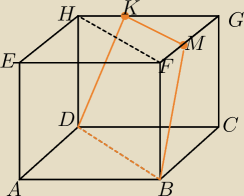
To jest zadanie trudne, odpuść go na razie.
Rozwiązuj proste zadania.
1) W graniastosłupie prawidłowym czworokątnym suma długości jego krawędzi jest równa 68cm, a
pole powierzchni całkowitej wynosi 190 cm
2 . Oblicz długość krawędzi graniastosłupa.
2). Znajdź długość boku podstawy i wysokości czworokątnego graniastosłupa prawidłowego,
wiedząc, że jego wysokość jest o 5 cm dłuższa od krawędzi podstawy, oraz że pole powierzchni
całkowitej graniastosłupa wynosi 800cm
2 .
3) Oblicz objętość sześcianu, wiedząc, że jego przekątna ma długość 6
√3.
30 sty 16:54
Saizou :
dasz radę
bezendu
W graniastosłupie prostym podstawa jest równoległobok o bokach a i b oraz o kacie ostrym alfa.
Znaleźć objętość graniastosłupa jeśli wiadomo ze mniejsza przekątna graniastosłupa równa się
większej przekątnej podstawy .
literki które mogą zostać w wzorze
V=P
p*H
no i teraz tak jak napisałeś z tw. cosinusów obliczmy d
d
2=a
2+b
2−2abcosα
d=
√a2+b2−2abcosα
pomyśl jak obliczyć H

i pole podstawy

30 sty 16:55
Saizou : zapomniałem wpisać literek które mogą zostać

a to literki : a,b,α
30 sty 16:57
bezendu:
3. a
√3=6
√3
V=6
3=216
30 sty 17:01
Saizou : 
30 sty 17:07
bezendu:
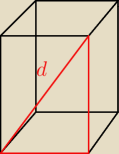
a
2+(a+5)
2=d
2
a
2+a
2+10a+25=d
2
d
2=2a
2+10a+25
i nic.
30 sty 17:09
Mila:
Bezendu, pisz nr zadania i na rysunku oznaczenia wierzchołków. jeśli mam Ci pomóc.
30 sty 17:21
bezendu:
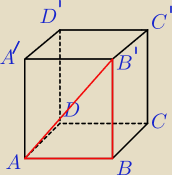
2)
30 sty 17:24
Mila:
Pc=800cm2
AB=a
BB'=H
H=a+5
Ktoś to pole obliczył, jak?
Pc=2a2+4*(a*H) teraz działaj.
30 sty 17:27
bezendu:
2Pp+4Pb=800
2a2+4(a2+5a)=800
2a2+4a2+20a=800
6a2+20a−800=0/ :2
3a2+10a−400=0
√Δ=70
a=10
30 sty 17:35
Mila:
h=a+5=15
Teraz1) Opieramy sie na rysunku z 17:24.
30 sty 17:57
bezendu:
2x+4y=68
x=34−2y
2Pp+4Pb=190
2(34−2y)2+4(34y−2y2)=190
2(1156−136y+4y2)+136y−8y2=190
2312−272y+8y2+136y−8y2=190
136y=2122
chyba coś nie tak?
30 sty 18:05
bezendu:
Nie wiem gdzie jest błąd.
30 sty 18:13
Mila:
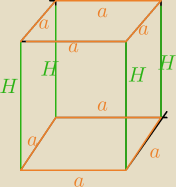
Masz 8 krawędzi o długości a i 4 boczne H
Wzór na P
c taki, jak 17:27
Cztery ściany boczne sa prostokątmi o wymiarach a i H.
30 sty 18:19
bezendu:
Czyli
4H+8a=68 /4
H+2a=17
H=17−2a
2P
p+4P
b=190
2a
2+4(17a−2a
2)=190
2a
2+68a−8a
2−190=0
−6a
2+68−190=0
3a
2−34+95=0
Δ=16
√Δ=4
30 sty 18:29
bezendu: ?
30 sty 19:20
Mila-bis:
Gdzie dokończenie, a weryfikację poprawności na maturze jak byś przeprowadził?
Mam całą serię zadan wprowadzających.
Czekam.
30 sty 19:42
bezendu:
a
1=5
H
1=17−2*5
H
1=7
30 sty 19:57
zawodus: teraz raczej ok
30 sty 20:00
Mila:
Sprawdź chociaż jeden warunek− na sumę krawędzi.
30 sty 20:01
bezendu:
4*7+8*5=68
Ale zanim wstawiłem rozwiązanie to sprawdziłem oba warunki.
30 sty 20:03
Mila:
4)
| | π | |
Podstawą graniastosłupa prostego jest romb o boku długości a i kącie ostrym α = |
| . |
| | 3 | |
Wysokość graniastosłupa również ma długość a. Oblicz dlugość przekątnych tego graniastosłupa.
5) .Podstawą graniastosłupa jest sześciokąt foremny o boku długości a, ściany boczne są
kwadratami. Oblicz długość przekątnych tego graniastosłupa.
30 sty 20:04
bezendu:
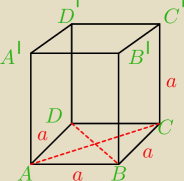
4)
|AC|
2=a
2+a
2−(2*a*a*cos60
0)
|AC|
2=2a
2−a
2
|AC|
=a
2
|AC|=a
|BD|
2=a
2+a
2−2(a*a*cos120
0)
|BD|
2=2a
2+a
2
|BD|
2=3a
2
|BD|=
√3a
|BD'|
2=a
2+(
√3a)
2
|BD'|
2=a
2+3a
2
|BD'|
2=4a
2
|BD|=2a
|AC'|
2=a
2+a
2
|AC'|=2a
2
|AC'|=
√2a
30 sty 20:19
Mila:
dobrze.
Powwinieneś narysować obok romb ABCD, narysować przekatne graniastosłupa, napisać która
dłuższa.
30 sty 20:25
bezendu:
Dobrze, a mogę prosić o rysunek do drugiego, bo nie mogę tutaj narysować w edytorze. Na kartce
nie mam problemu.
30 sty 20:26
Mila: Tak.
30 sty 20:30
Mila:
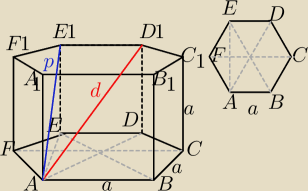
30 sty 20:36
bezendu:
|AD|=2a
|DD1|=a
|AD1|2=|AD|2+|DD1|2
|AD1|2=4a2+a2
|AD1|=√5a
|AE|=a√3
|EE1|=a
|AE1|2=|AE|2+|EE1|2
|AE1|2=(a√3)2+a2
|AE1|2=4a2
|AE1|=2a
30 sty 20:41
Mila:
Oblicz objętość i Pb ,
dla a=6
30 sty 20:50
Mila:
Potem załóż nowy wątek, będą gran. trójkatne.
30 sty 20:50
bezendu:
A mogę od razu skorzystać z tych przekątnych dla sześciokąta formnego, czy mam wyprowadzać tę
przekątne?
30 sty 20:52
Mila:
to jest cd. korzystaj.
30 sty 20:54
bezendu:
P
b=6*a
2
P
b=6
3=216
V=9
√3*6=54
√3
30 sty 20:56
Mila:
| | 62√3 | |
Psześciokata=6*PΔ=6* |
| =... |
| | 4 | |
30 sty 21:00
bezendu:
Pp=54√3
V=6*54√3=324√3
Dziękuję za zadania i poprawki.
30 sty 21:02
Mila:
To jeszcze jedno, do rysunku gran. sześciokątnego.
Czy choć trochę rozjaśnia się .
Oblicz długość krótszej przekątnej i pole powierzchni bocznej prawidłowego graniastosłupa
sześciokątnego, jeżeli długość jego najdłuższej przekątnej wynosi 13dm, a krawędzi podstawy
długość 5dm.
30 sty 21:08
bezendu:
Bardzo się rozjaśnia. Dziękuję to chyba za małe słowo

Już się biorę do liczenia.
30 sty 21:12
Marcin: 10
2+h
2=13
2 Zadanie wydaje się przyjemne

30 sty 21:18
bezendu:
H2=132−102
H2=69
H=√69
Pb=6*(p{69*5)
Pb=30√69dm2
d−krótsza przekątna
d2=(5√3)2+(√69)2
d2=144
d=12
30 sty 21:23
Mila:
Dobrze.
Na dzisiaj wystarczy bryłek. Jutro dalej ćwiczymy.
Dobranoc.
30 sty 21:29
bezendu:
Dziękuję

Dobranoc.
30 sty 21:30
 jeśli mam gra.pra czw to w tym trójkącie nie będzie kątów prostych ?
jeśli mam gra.pra czw to w tym trójkącie nie będzie kątów prostych ?
 d=a√2 jako przekątna kwadratu
l=√a2+H2 z tw. Pitagorasa
gdyby miał być kąt prosty to α musi być tym kątem
l2+l2=d2
2l2=d2
2√a2+H2=(a√2)2
2a2+2H2=2a2
H=0 co jest sprzeczne zatem nie może być tam kąta prostego
d=a√2 jako przekątna kwadratu
l=√a2+H2 z tw. Pitagorasa
gdyby miał być kąt prosty to α musi być tym kątem
l2+l2=d2
2l2=d2
2√a2+H2=(a√2)2
2a2+2H2=2a2
H=0 co jest sprzeczne zatem nie może być tam kąta prostego


 łap zadanko
Jaką objętość ma czworościan foremny o krawędzi długości a
łap zadanko
Jaką objętość ma czworościan foremny o krawędzi długości a



 ale czy wysokość całej bryły jest równa wysokości np. podstawy ?
ale czy wysokość całej bryły jest równa wysokości np. podstawy ?
 Najpierw rysunek:
Najpierw rysunek:

 zatem V=?
zatem V=?
 i teraz pitagoras aby obliczyć H jako wysokość bryły
i teraz pitagoras aby obliczyć H jako wysokość bryły 



 x2=a2+b2−2(a*b*cos(180−α))
x2=a2+b2−(2ab*(−cosα))
x2=a2+b2+2abcosα
x=√a2+b2+2abcosα
I dalej nie wiem dokończę jak wrócę ze szkoły.
x2=a2+b2−2(a*b*cos(180−α))
x2=a2+b2−(2ab*(−cosα))
x2=a2+b2+2abcosα
x=√a2+b2+2abcosα
I dalej nie wiem dokończę jak wrócę ze szkoły.
 To jest zadanie trudne, odpuść go na razie.
Rozwiązuj proste zadania.
1) W graniastosłupie prawidłowym czworokątnym suma długości jego krawędzi jest równa 68cm, a
pole powierzchni całkowitej wynosi 190 cm 2 . Oblicz długość krawędzi graniastosłupa.
2). Znajdź długość boku podstawy i wysokości czworokątnego graniastosłupa prawidłowego,
wiedząc, że jego wysokość jest o 5 cm dłuższa od krawędzi podstawy, oraz że pole powierzchni
całkowitej graniastosłupa wynosi 800cm2 .
3) Oblicz objętość sześcianu, wiedząc, że jego przekątna ma długość 6√3.
To jest zadanie trudne, odpuść go na razie.
Rozwiązuj proste zadania.
1) W graniastosłupie prawidłowym czworokątnym suma długości jego krawędzi jest równa 68cm, a
pole powierzchni całkowitej wynosi 190 cm 2 . Oblicz długość krawędzi graniastosłupa.
2). Znajdź długość boku podstawy i wysokości czworokątnego graniastosłupa prawidłowego,
wiedząc, że jego wysokość jest o 5 cm dłuższa od krawędzi podstawy, oraz że pole powierzchni
całkowitej graniastosłupa wynosi 800cm2 .
3) Oblicz objętość sześcianu, wiedząc, że jego przekątna ma długość 6√3.
 dasz radę bezendu
W graniastosłupie prostym podstawa jest równoległobok o bokach a i b oraz o kacie ostrym alfa.
Znaleźć objętość graniastosłupa jeśli wiadomo ze mniejsza przekątna graniastosłupa równa się
większej przekątnej podstawy .
literki które mogą zostać w wzorze
V=Pp*H
no i teraz tak jak napisałeś z tw. cosinusów obliczmy d
d2=a2+b2−2abcosα
d=√a2+b2−2abcosα
pomyśl jak obliczyć H
dasz radę bezendu
W graniastosłupie prostym podstawa jest równoległobok o bokach a i b oraz o kacie ostrym alfa.
Znaleźć objętość graniastosłupa jeśli wiadomo ze mniejsza przekątna graniastosłupa równa się
większej przekątnej podstawy .
literki które mogą zostać w wzorze
V=Pp*H
no i teraz tak jak napisałeś z tw. cosinusów obliczmy d
d2=a2+b2−2abcosα
d=√a2+b2−2abcosα
pomyśl jak obliczyć H  i pole podstawy
i pole podstawy 
 a to literki : a,b,α
a to literki : a,b,α

 a2+(a+5)2=d2
a2+a2+10a+25=d2
d2=2a2+10a+25
i nic.
a2+(a+5)2=d2
a2+a2+10a+25=d2
d2=2a2+10a+25
i nic.
 2)
2)
 Masz 8 krawędzi o długości a i 4 boczne H
Wzór na Pc taki, jak 17:27
Cztery ściany boczne sa prostokątmi o wymiarach a i H.
Masz 8 krawędzi o długości a i 4 boczne H
Wzór na Pc taki, jak 17:27
Cztery ściany boczne sa prostokątmi o wymiarach a i H.
 4)
|AC|2=a2+a2−(2*a*a*cos600)
|AC|2=2a2−a2
|AC|=a2
|AC|=a
|BD|2=a2+a2−2(a*a*cos1200)
|BD|2=2a2+a2
|BD|2=3a2
|BD|=√3a
|BD'|2=a2+(√3a)2
|BD'|2=a2+3a2
|BD'|2=4a2
|BD|=2a
|AC'|2=a2+a2
|AC'|=2a2
|AC'|=√2a
4)
|AC|2=a2+a2−(2*a*a*cos600)
|AC|2=2a2−a2
|AC|=a2
|AC|=a
|BD|2=a2+a2−2(a*a*cos1200)
|BD|2=2a2+a2
|BD|2=3a2
|BD|=√3a
|BD'|2=a2+(√3a)2
|BD'|2=a2+3a2
|BD'|2=4a2
|BD|=2a
|AC'|2=a2+a2
|AC'|=2a2
|AC'|=√2a

 Już się biorę do liczenia.
Już się biorę do liczenia.

 Dobranoc.
Dobranoc.