proszę o rozwiązanie michał: Pole trapezu wynosi 169 . Punkt przecięcia przekątnych dzieli każdą przekątną na dwa odcinki, których długości pozostają w stosunku 5:8. Oblicz pola trójkątów, na jakie przekątne podzieliły trapez.

pigor: ..., szukane pola to : 5*8=40, 40, 8*8=64, 169−144= 25 . ...

michał: ale dlaczego tak można rozwiązać, na jakiej podstawie

5-latek:

Pudel: Rozwiąż np.układ równań:

⎧	0,5[a2b1]sinα=S1
⎜	0,5[a1b1]sin(180−α)=S2
⎨	0,5[a1b2]sinα=S3
⎩	0,5[a2b2]sin(180−α)=S4

	a2		5		b1		5
&		=		&		=		&S1+S2+S3+S4=169
	a1		8		b2		8

Rysunek sugeruje trapez równoramienny ale...

Mila:

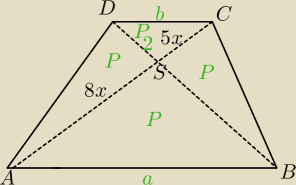
	b		SC		3
ΔDCS∼ΔABS w skali k=		=		=
	a		AS		5

Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa⇔

P2		5
	=(		)2⇔
P1		8

P2		25
	=
P1		64

	25
P2=		P1
	64

	5
PΔCSB=PΔDSA=		P1
	8

	5		25
2*		P1+P1+		P1=169
	8		64

P₁=64

	25
P2=		*64=25
	64

	5
P=		*64=40
	8