Prawdopodobieństwo.
Marcin: W jadalni znajduje się okrągły stół, przy którym może usiąść 6 osób. Pod ścianą stoi ława, na
której
również może usiąść 6 osób. Do jadalni wchodzi 6 osób, które najpierw w sposób losowy usiądą
przy
stole, a następnie na ławie.
Które z prawdopodobieństw jest większe: prawdopodobieństwo tego, że M i R będą sąsiadami,
siadając przy stole, czy prawdopodobieństwo tego, że M i R będą sąsiadami, siadając na ławie?
Jakieś pomysły? Czy Ω w jednym i drugim przypadku będzie równa 6!?
29 sty 20:28
wredulus_pospolitus:
Ω może być taka sama tu i tu, pod warunkiem że odpowiednio ją opiszesz
zauważ, że:
stół jest okrągły −> miejsca nie są numerowane (w zamyśle)
więc Ω może być zbudowana przy stwierdzeniu, że miejsca nie są numerowane, ale także może być,
że jednak są numerowane (odpowiednio zwiększy się wtedy #A)
29 sty 20:48
Eta:
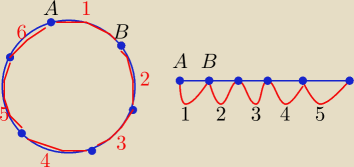
|Ω|=6! ( dla obydwu sytuacji)
Przy stole : 2!(zmiany AB , BA) i 6 miejsc do wyboru i pozostałe 4 osoby na 4!
|A|=2*6*4!
Przy ławie 2!*5 *4!
|A|= 2*5*4!
i............

29 sty 20:50
Marcin: Wielkie dzięki za wytłumaczenie

29 sty 20:55
 |Ω|=6! ( dla obydwu sytuacji)
Przy stole : 2!(zmiany AB , BA) i 6 miejsc do wyboru i pozostałe 4 osoby na 4!
|A|=2*6*4!
Przy ławie 2!*5 *4!
|A|= 2*5*4!
i............
|Ω|=6! ( dla obydwu sytuacji)
Przy stole : 2!(zmiany AB , BA) i 6 miejsc do wyboru i pozostałe 4 osoby na 4!
|A|=2*6*4!
Przy ławie 2!*5 *4!
|A|= 2*5*4!
i............ 
