. Piotr 10: W czworościanie ABCD długość krawędzi |AB|=6, |CD|=2 a pozostałe krawędzie mają tę samą długość równą 4. Oblicz objętość oraz sumę kwadratów cosinusów kątów nachylenia krawędzi bocznych do płaszczyzny podstawy ABC. Gdzie będzie leżał spodek wysokości ostrosłupa i dlaczego?

Piotr 10: Hmm ?

zawodus: dobrze przepisałeś treść?

Piotr 10: Yhym 100%

Piotr 10: Nie wiem jak ten środek znaleźć, może ten czworościan jest symetryczny ?

Mila: No to jest piękne zadanie. Spodek będzie leżał na wysokości ΔABC, który jest równoramienny : 6,4,4. Zrób rysunek z oznaczeniami.

zawodus: jest symetryczny sporo liczenia jest Wysokość znajduje się na wysokości podstawy trójkąta ABC. Można oznaczyć ją CD

zawodus: ale posiadam nawet odpowiedź jakby co... tylko pokażę po skończeniu przez ciebie

Mila: Czworościan ma płaszczyznę symetrii przechodzącą prrzez D i wysokość ΔABC opuszczoną na AB.

Piotr 10: Nie wiem czy dzisiaj to zrobię, bo mam dość już tych ostrosłupów.. A możecie mi powiedzieć czy zadania z walcami, stożkami i kulami są łatwiejsze niż ostrosłupy Czy ciężko określić ?

zawodus: Wpisywanie kuli i opisywanie jest najtrudniejsze. Reszta jest prosta.

Piotr 10: Bo na razie to z ostrosłupami średnio mi idzie.

wredulus_pospolitus: Piotr ... na dobrą sprawę te wszystkie zadania sprowadzają się do dwóch rzeczy: 1) dobry rysunek (+ umiejętność wyobrażenia sobie tego w 3D) 2) zauważenia trójkątów prostokątnych opanujesz te dwie rzeczy ... każde zadanko będzie 'do pyknięcia'

zawodus: tylko wyobraźnia 3D to zaawansowana umiejętność

Piotr 10: No może dla Ciebie to tak, ale myślałem na początku, że stereometria nie będzie taka trudna, bo lubię geometrię analityczną i geometrię na płaszczyźnie, a tu się okazało, że jednak jest dla mnie trudna. W szczególności ostrosłupy,

wredulus_pospolitus: Piotr ... spokojnie ... przerobisz 30 zadań z ostrosłupów to będzie je 'pykał' z zamkniętymi oczami, wyobrażając sobie dokładnie jak przecinają daną figurę płaszczyzny czy inne rzeczy które się mogą tam pojawiać

zawodus: Piotrek, a może chcesz to zadanie? już je kiedyś widziałem w necie...

Piotr 10: Już przerobiłem ponad 30 dobre, i co prawda chyba już lepiej to ogarniam. Zadania z ostrosłupów z matur CKE wydają mi się łatwiejsze niż te co robię. Tamte zadania nie sprawiały mi aż dużego problemu w porównaniu do tych co przerabiam

Piotr 10: zawodus nie nie, sam spróbuję jutro zrobić, bo muszę zająć się innymi przedmiotami, także dziękuję wam za pomoc.

zawodus: spoko jak chcesz jak coś to pisz

Piotr 10: zawodus jeśli posiadasz odpowiedź to jakbyś mógł sprawdź moje wyniki: V=2√6 Zaś suma kwadratów cosinusów kątów nachylenia krawędzi bocznych do

	5
płaszczyzny podstawy ABC wynosi S= 1
	7

Mila: Wczoraj policzyłam, wyrzuciłam kartkę, jak kolega nie napise, to policzę jeszcze raz.

Piotr 10: OK

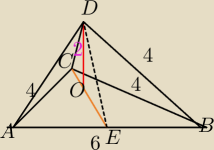
Mila: DE=CE=√7 ΔCED− Δ równoramienny

	2√6
H=|OD|=		z porownania pola ΔCED
	√7

P_ΔABC=3√7 V=2√6

Piotr 10: Wyszło, super