.
Piotr 10: W ostrosłupie prawidłowym czworokątnym wysokość h=30, krawędź podstawy wynosi 20. Przez krawędź
podstawy poprowadzono płaszczyznę prostopadła do przeciwległej ściany bocznej. Oblicz pole
otrzymanego przekroju.
Znów problem... jak ten przekrój wygląda ?
29 sty 16:38
29 sty 16:40
zawodus: przekrój jak widać to trapez równoramienny
29 sty 16:40
Piotr 10: błąd wyskakuje mi przy linku ktory podales
29 sty 16:47
29 sty 16:48
Piotr 10: nie

29 sty 16:50
29 sty 16:53
zawodus: sprawdź teraz
29 sty 16:53
Mila:
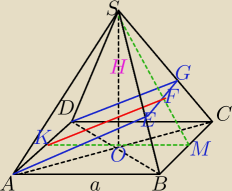
29 sty 16:56
Mila:
KF⊥FS
29 sty 16:57
Piotr 10: Hmm i od czego zacząć te zadanie ?
29 sty 17:03
zawodus: "Wytnij" z rysunku MILI trójkąty KMS oraz BCS.
To wystarczy, żeby policzyć wysokość trapezu (z KMS) oraz drugą podstawę (z BCS)
liczysz

29 sty 17:05
Mila:
PΔKMS na dwa sposoby.
KF jest wysokością przekroju i wysokością ΔKMS opuszczona na ramię SM.
29 sty 17:09
zawodus: Mila daj mu pomyśleć

29 sty 17:12
Mila:
Porzucam Was

29 sty 17:14
Piotr 10: zawodus liczyłeś to może ? Masz odpowiedź ?
29 sty 17:40
zawodus: nie liczyłem, ale jak znajdę chwilkę to policzę. Jak zwykle nie masz odpowiedzi?
29 sty 17:47
Piotr 10: no nie mam ; d . Mam problem z obliczeniem górnej podstawy trapezu. wysokość już policzyłem
29 sty 17:49
Piotr 10: z podobieństwa trójkątów trzeba skorzystac ?
29 sty 17:50
Mila:
Tak.
P=108√10
29 sty 18:33
zawodus: można tylko potrzebny jeden z odcinków SF i FM

29 sty 18:33
Piotr 10: Mila super też mam taki wynik

. Dziękuję Wam za pomoc

29 sty 18:43






 . Dziękuję Wam za pomoc
. Dziękuję Wam za pomoc 