Pola trójkątów ech: Wykaż, że pola czterech trójkątów, na które przekątne dzielą równoległobok, są równe

Aga1.:

	1
P1=		xysinα
	2

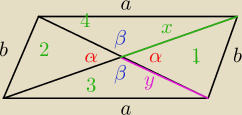
Przekątne w równoległoboku dzielą się wzajemnie na połowy. P₂=P₁, bo są to trójkąty przystające

	1		1		1
P3=		xy*sinβ=		xy*sin(1800−α)=		xy*sinα.
	2		2		2

P₃=P₄ ,bo są to trójkąty przystające.(Z czego to wynika?)

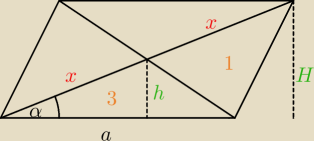
wredulus_pospolitus: Można tez inaczej: P3 = P4 <−−− trójkąty przystające P2 = P1 <−−− trójkaty przystające

	P3+P1
wykażemy, że P3 = P1 .... a konkretniej, że:		= P3
	2

wiemy, że przekątne przecinając się, dzielą się na pół (stąd x) z tw. Talesa

x		2x
	=		−> H = 2*h
h		H

	a*h
P3 =
	2

	a*H		a*2h		P3+P1
(P1 + P3) =		=		= a*h = 2*P3 =>		= P3 => P1 = P3
	2		2		2

c.n.w.

pigor: ..., albo dlatego, że wszystkie 4 trójkąty, to trójkąty o równych wysokościach względem jednakowych podstaw − połówek dłuższej (lub krótszej) przekątnej ....