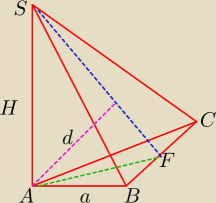
W ostrosłupie ABCS podstawa ABC jest trójkątem równobocznym o boku długości a. Krawędź AS jest
prostopadła do płaszczyzny podstawy. Odległość wierzchołka A od ściany BCS jest równa d.
Wyznacz objętość tego ostrosłupa.
to tak:
| a√3 | ||
IAFI= | ; ISFI=x | |
| 2 |
| H*IAFI | ||
d= | ||
| x |
| a*H*√3 | ||
x= | ||
| 2d |
| a√3 | ||
H2+( | )2=x2 | |
| 2 |
| 3a2 | 3H2a2 | |||
H2+ | = | |||
| 4 | 4d2 |
| 12(ad)2 | ||
H2= | ||
| 4(3a2−4d2) |
| 2√3ad | ||
H= | ||
| 2√3a2−4d2 |
| 1 | a2√3 | 2√3ad | a3*d | |||||
V= | * | * | = | |||||
| 3 | 4 | 2√3a2−4d2 | 4√3a2−4d2 |
