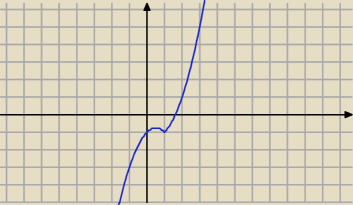
pa Radek: Dla jakich wartości parametru m równanie x|x−1|=m+1 ma dwa różne rozwiązania? x|x−1|−1=m o to chodzi ?

Godzio: Tak, teraz określ kiedy proste y = m przecinają wykres w dwóch różnych miejscach.

Radek: dla m=−1

Godzio: m ∊ <x₁,x₂>, gdzie x₁,x₂ − wierzchołki obu parabol (tak z rysunku wynika)

ZKS: m ∊ {x₁ ; x₂}

Mila: Wg Twojego wykresu: 1) m+1=−1⇔m=−2

	1		1		3
2) m+1=yw ( yw=		*|		−1|−1=−		⇔
	2		2		4

	3
m+1=−		⇔....
	4

Dobranoc.

Radek: Dobranoc.

Radek: To coś nie tak z tym wykresem ?

Godzio: No jasne, chodziło mi o same punkty, a nie o przedział

Radek: a co z nim nie tak ?

Godzio: W przedziale (x₁,x₂) masz 3 rozwiązania, a nie dwa.

Radek: Dzięki

Radek: ale czemu mając x|x−1|=m+1 nie mogę zrobić x|x−1|−1=m ?

Godzio: Możesz, nikt tego nie kwestionował

Mila: Źle napisałam 23:24, nie zauważyłam, że na wykresie jest wykres funkcji f(x)=x*|x−1|−1 To jakie masz wartości dla m?

Radek: To już sam nie wiem jak mam to wyznaczyć?

Mila: Jedną masz dobrze, chodzi mi o drugą wartość parametru m. Mam narysować?

Radek: Tak.

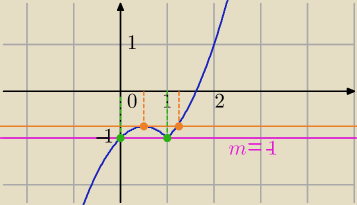
Mila: Dla jakich wartości parametru m równanie x|x−1|=m+1 ma dwa różne rozwiązania? f(x)=x*|x−1|−1 x*|x−1|−1=m ma dokłane dwa rozwiązania dla m=−1 jest przecięcie wykresu f(x) w dwóch punktach

	3
m=−		jest przecięcie wykresu f(x) w dwóch punktach
	4

	3
yw=−		druga wsp. wierzchołka paraboli w przedziale (0,1)
	4

Policz x_w i y_w dasz radę?

Radek: Ale Pani już policzyła y_w ?

Mila: W takim razie , wszystko jasne?

Radek: Jeszcze mam pytanie czemu y_w ma być w przedziale?

zawodus: spójrz na rysunek. w przedziale (0,1) mamy maksimum lokalne

Radek: dziękuję.