Pazdro bezendu: Mam do rozwiązania nierówność

1		1		1
	+		+		<0
x(x+1)		(x+1)(x+2)		(x+2)(x+3)

D=R\{−3,−2,−1,0}

	1		1		1
Mam pisać, że korzystam ze wzoru		=		−		, czy od razu mogę rozwiązać ?
	n(n+1)		n		n+1

1		1		1		1		1		1
	−		+		−		+		−		<0
x		x+1		x+1		x+2		x+2		x+3

1		1
	−		<0
x		x+3

3x(x+3)<0 x∊(−3,−2)∪(−2,−1)∪(−1,0)

bezendu: ?

a: NIE

bezendu: Wole, żeby ktoś inny się wypowiedział.

mix: ok można też rozwiązanie zapisać tak: x∊(−3,0)\{−1,−2}

bezendu: Ale to jest równoważny zapis przecież. I nawet taki mam w odpowiedziach.

mix:

bezendu: Dziękuję.

Mila: Możesz nie pisać, możesz natomiast zapisać znak⇔

bezendu: Mila ale gdzie ten znak postawić ?

zawodus: przy przejściu z jednej linii do drugiej

bezendu: Dziękuję . A odnośnie brył nie będę wstawiał zadań bo wstawianie po 50 zadań mija się z celem.

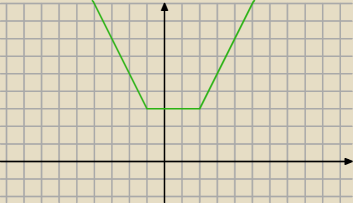
bezendu: Wyznacz zbiór rozwiązań równania |x+1|+|x−2|=p w zależności od parametru p p∊R (−∞,−1) −2x+1 <−1,2) 3 <2,∞) 2x−1 p∊(−∞,3) brak rozwiązań p∊{3} jedno rozwiązanie p∊(3,∞) dwa rozwiązanie Ale w odpowiedzi jakoś inaczej ?

Piotr 10: dla p=3 nieskończenie wile rozwiązań

bezendu: no tak pomyłka ale to i tak nie jest poprawnie

mix: dla p=3 −− nieskończenie wiele rozwiązań

Piotr 10: To weź zobacz czy dobrze wyliczyłeś wcześniej, tak gdzieś musi tkwić błąd zapewne

bezendu: Tak, wiem ale to wszystko jest źle.

bezendu: Dobrze wyliczyłem, bo sprawdzałem.

zawodus: co jest źle?

zawodus: co jest źle?

bezendu: Moje rozwiązanie, nawet z poprawką mix.

zawodus: a jaka jest niby odpowiedź?

bezendu: Na pewno nie taka jak ja podałem.

zawodus: Odpowiedź jest pewnie taka: Dla p<3 x = ∅

	1−p		p−1
Dla p>3 x∊{		;		}
	2		2

Dla p=3 x ∊<−1;2>

bezendu: No jak byś spisał z mojego arkusza. Tylko czemu taka ?

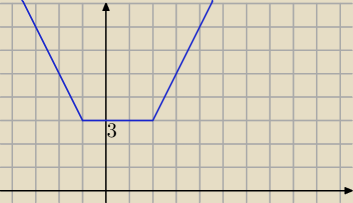
mix: pamiętaj,że p≥0 !

bezendu: To pierwsze i ostatnie jestem w stanie zrozumieć, ale środkowy warunek niezrozumiały jest dla mnie.

bezendu: I czemu teraz to p≥0 ?

mix: |x+1|+|x−2|≥0 ..... jasne?

bezendu: |x+1|+|x−2|=p Ale po narysowaniu to jest tylko>0 a czemu warunek ≥ ?

zawodus: nie słuchaj tylko napisz tak ja ja podałem...

zawodus: dla x ∊ (−∞,−1) liczysz rozwiązanie dla x∊ (2,+∞) liczysz rozwiązanie

Mila: Nie pytają Cię, ile rozwiązań ma równanie lecz jakie w zależności od parametru p.

bezendu: Trudno nie słuchać Ety chyba nauczyciel zawsze ma rację, ale sam nie wiem po co to p≥0 I wytłumacz ten drugi warunek, bo nie chcę przepisywać bez zrozumienia.

bezendu: ?

mix: Tym razem wprowadziłam Cię w błąd, nie doczytałam treści Zobacz co napisała Mila

bezendu: Wiem co napisała Mila, ale nie rozumiem zapisu tego drugiego warunku.

bezendu: ?

ZKS: No jak nie rozumiesz? Dla x ∊ (−∞ ; −1) otrzymujesz równanie postaci −x − 1 − x + 2 = p −2x = p − 1

	1 − p
x =		to jest Twoje rozwiązanie równania dla x ∊ (−∞ ; −1).
	2

Tak samo robisz dla pozostałych x. Najzwyczajniej w świecie rozwiązujesz równanie ze zmienna x.

bezendu: I trzeba było tak od razu pisać ! Dziękuję.

mix: miałeś funkcję 3 dla x∊<−1, 2) 2x−1 dla x ≥2 −2x+1 dla x <−1 dla p>3 −2x+1= p ⇒x=.... i 2x−1=p ⇒ x=....

bezendu: Eta dziękuję, już wiem o co chodzi.