F kwadratowa. (nierówności) Justa: Drodzy Matematycy! Proszę o wskazówki w rozwiązaniu zadania, bo mam wrażenie, że mózg mi gdzieś wywiało.. i wszystko się miesza w pustej głowie. A mianowicie mowa tu o zadaniu o następującej treści: Rozwiąż nierówność: |x²−x|−|x−5|≤3 i moje pytanie tak na sam początek: 1) czy mogę rozwiązać to zadanie wyznaczając miejsca zerowe czyli z x²−x →f(1)=0; f(0)=0 i z x−5 →f(5)=0 a następnie określić dzięki nim przedziały 1^o (−∞;0) 2^o <0;1) 3^o <1;5) 4^o <5;+∞) i rozpatrzeć daną nierówność w tych 4 przypadkach? czy jestem w błędzie?

Bizon: ... ciepło ... ciepło −

Justa: hmmm.. to tyle dobrego, a w czym tkwi błąd mojego rozumowania ?

Bizon: więcej wiary w Siebie −

Justa: ok, wzięłam sobie dobrą radę do serca i zrobiłam tak : 1^o x∊(−∞:0) x²−x−(−x+5)≤3 x²≤8 x∊<−2√2; 2√2> uwzględniając to z założeniem x∊<−2√2;0) 2^o x∊<0;1> x²−x−(−x+5)≤3 x²≤8 x∊<−2√2; 2√2> uwzględniając to z założeniem x∊<0;1) 3^o x∊<1;5) x²−x−(−x+5)≤3 x²≤8 x∊<−2√2; 2√2> uwzględniając to z założeniem x∊ <1;2√2> 4^o x∊<5;+∞) x²−x−x+5≤3 x²≤−2 ←sprzeczne. Rozwiązanie końcowe: X∊<−2√2;2√2> dobrze ? czy czegoś brakuje?

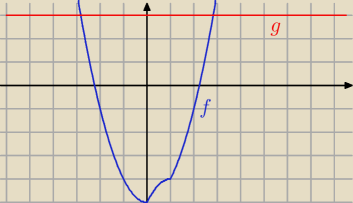
Mila: f(x)=|x²−x|−|x−5| g(x)=3 w przedziale <0,1) masz taką nierówność: −x²+2x−8≤0 Δ<0 funkcja przyjmuje tylko wartości ujemne w tym przedziale x∊<0,1) odp, dobra

Justa: hmmm.. x∊<0;1) |x²−x| → i gdy podstawie jako x=0 → otrzymam |0| byłam przekonana, że zero w wartości bezwzględnej może być i wtedy bez zmian. ale dziękuję.

Mila: Tak , dla zera jest dobrze, ale dalej nie. To ma być przedział (0,1) .( Ze względu na |x²−x| ) Przedziały mają być takie: (−∞,0> (0,1) <1,5) <5,∞)

Justa: <o:1) gdy podstawię np. ¹₂ →|(¹₂)²−¹₂| =|−¹₄| faktycznie. dziękuję

Mila: Justa przedział (0,1), z funkcją kwadratową w |..| trzeba uważać.

Justa: dzięki dzięki Rada, na pewno się przyda ; )

Mila: