oblicz sumę Matejko: oblicz sumę pięćdziesięciu najmniejszych dodatnich rozwiązań równania a) cos³x=cosx cosx(cos²x−1)=0 cosx=0 cosx=1 cosx=−1 jak to szybko obliczyć?

Matejko: ?

PW: Szybko to znaczy jak? Normalnie − wypisz wszystkie serie rozwiązań, odrzuć z nich liczby ujemne i zero, zostaw 50 najmniejszych dodatnich

Matejko: mógłbym prosić żeby ktoś to policzył?

Bizon: to zapytam Cię tak? ...a jakie są te dodatnie rozwiązania tego równania ?

Matejko: cosx=0 dla ^pi₂, ^3pi₂...... cosx=1 dla 0,2pi........... cosx=−1 dla pi,3pi.........

KUZDE: cos x = 0 dla pi/2 + 2k* pi v 3/2pi + 2k*pi cos x = 1 dla 0 + 2k*pi cos x = −1 dla pi + 2k*pi od < 0 do 2pi ) ( w nastepnych tak samo ) mamy 4 rozwiazanie rowne 3pi + 8*k*pi , k ∊ N wiec pierwsze 48 rozwiazani miesci sie w pierwszych 12 "przedziałach" suma = 12 * 3pi + 8pi ( 0 + 1 + 2 + ... + 10 + 11 ) kolejne 2 rozwiazania to pi/2 i pi dla k = 12 suma tych 2 rozwiazan to 3/2pi + 4*12

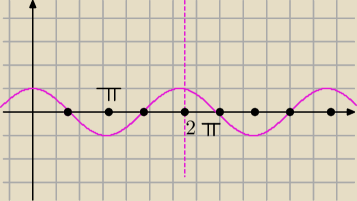
Mila: Rozwiązania to kolejne wyrazy ciągu arytmetycznego:

	π
a1=
	2

	π
r=
	2

	π		π
a50=		+49*		=25π
	2		2

S₅₀= ... oblicz