wyznacz wartosci parametru m dla ktorych rownanie ma nieskonczenie wiele roz marcin: wyznacz wartosci parametru m dla ktorych rownanie |x−m|+|x−7| = 3 ma nieskonczenie wiele rozwiazan gdyby ktoś mógł krok po kroku wyjaśnić jak podchodzić do tego typu zadań, byłbym bardzo wdzięczny. wychodzą mi cuda na kiju w żaden sposób niepowiązane z rozwiązaniem

marcin: bump

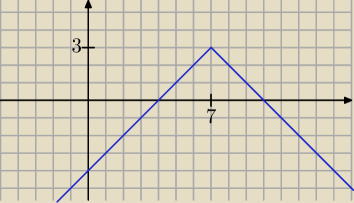
Bogdan: To jest wykres y = 3 − |x − 7| (*) |x − m| = 3 − |x − 7| y = 3 − |x − 7| i y = |x − m| dla x < 7: y = 3 + x − 7 = x − 4 dla x ≥ 7: y = 3 − x + 7 = −x + 10 Równanie (*) ma nieskończenie wiele rozwiązań wtedy, gdy proste wyrażone równaniem y = |x − m| pokryją się na dowolnej długości z prostą y = x − 4 lub z prostą y = −x + 10

marcin: wielkie dzięki Bogdan, chyba mniej więcej załapałem

pigor: ..., lub szukasz na osi OX takich x−ów, których suma odległości od m i 7 jest równa 3, czyli ⇔ m=4 v m=10 − szukane wartości m, wtedy przedziały [4;7] v [7;10] są rozwiązaniami danego równania odpowiednio.