W kolo wpisano prostokat. Znajdz najwieksze pole. Krzysztof Krawczyk: W koło o promieniu r wpisano prostokąt. Znajdź wymiary takiego prostokąta, który będzie miał największe pole. Proszę o pomoc !

Bogdan: Czy możesz stosować rachunek pochodnych?

pigor: .... , otóż , np. tak : niech α − miara kąta między przekątnymi długości e prostokąta wpisanego w koło o promieniu r, to jego pole P=¹₂e²sinα , ale e=2r, 0< sinα≤ 1, więc P=¹₂*(2r)²sinα= ¹₂*4r²sinα= 2r²sinα ≤ 2r², przy czym równość zachodzi ⇔ α=90^o, czyli prostokąt o największym polu jest kwadratem o boku a=r√2, bo 2r=a√2 ⇔ 2a=2√2r ⇔ a=r√2 ..

Bartek Kanapka: a na pochodnych jak to liczyć?

Krzysztof Krawczyk: Tak, zadanie polegać ma na rachunku pochodnych.

Ruda69: Przyłączam sie do pytania plisska *

J: P = x*y x,y boki prodstokąta, Z tw.Pitagorasa y² + x² = (2r)² czyli y = √4r² − x² Zatem P = f(x) = x*√4r² − x²

pigor: ..., no to włączając myślenie prostokąt opisany w zadaniu na pole wyrażone np. wzorem zmiennej [n[0≤ α ≤ ^π₂ takim: P(α)= u{1}{2)*4r²sinα , zatem pochodna P' (α)= 2r²cosα = 0 ⇔ cosα= 0 ⇒ α=^π₂=90^o i teraz dokończcie sami ładnie uzasadniając istnienie maksimum lokalnego w tym kącie α , że pochodna zmienia znak, albo z drugiej pochodnej P'' (α)= itd. .

Krzysztof Krawczyk: Ale pochodna z P(α)= u{1}{2)*4r2sinα jest równa 4r*sinα + 2r² *cosα

pigor: ... , oj studencie bzdety gadasz, przecież r= constans

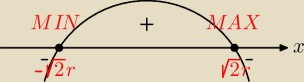
Bogdan: albo P(x) = √4r²x² − x⁴

	8r2x−4x3x		−2(x − √2r)(x + √2r)
P'(x)=		= ... =
	2√4r2x2 − x4		√4r2 − a2

P_max = P(√2r), x = √2r i y = √4r² − 2r² = r√2 = x, prostokąt jest kwadratem o boku rownym √2r

Krzysztof Krawczyk: Faktycznie, mój błąd! Dziekuję

Krzysztof Krawczyk: A mogę wiedzieć skąd się wzięło : P(x) = √4r² * x² − x⁴?

J: Popatrz na post 14:32 i włacz x pod pierwiastek.

Marcin: Nie rozumiem skąd się wzięło w liczniku pochodnej 8r²x−4x^3x. jak z 4r²3x²−2x wyszlo 8r²x−4x^3x

Bogdan: mały chochlik: zamiast 4x^3x ma być 4x³

Marcin: Juz sie wszystko zgadza