jednokładność
Radek:
Wytłumaczy ktoś jednokładność ?
Mam kilka zadań ale nie wiem czy wstawiać dlatego pytam
27 sty 23:09
Saizou: ja na pewno nie teraz bo jestem na telefonie, ale tam wystarczy tylko zapamietac 'tam gdzie nie
ma prima jest k' i po ptokach xd
27 sty 23:11
Radek: ale ja tego wgl nie rozumiem, nie wiem jak obliczać tę skalę
27 sty 23:16
Janek191:
Jednokładność o środku O = ( 0; 0) i skali s ≠ 0 opisuje układ równań:
x' = s*x
y' = s*y'
P = ( x; y) P' = ( x' ; y ' )
Jso : P → P'
27 sty 23:25
Radek:
A np mam pole dwóch trójkatów to jak wyznaczyć skalę ?
27 sty 23:25
Janek191:
Kliknij po lewej stronie na: geometria na płaszczyźnie
a następnie na : Jednokładność o środku O i skali k

27 sty 23:28
27 sty 23:29
Janek191:
W definicji jednokładności jest pomyłka

Powinno być y' = s*y
27 sty 23:31
Radek: Ale tam nie ma przykładowych zadań jak rozwiązać krok po kroku
27 sty 23:39
Janek191:
Ale jest podany sposób obliczania punktów jednokładnych do danych
w podanej skali

27 sty 23:43
Radek:
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu (x−16)22+y22 =
4 jest okrąg o równaniu (x−6 )2+(y−4)2 =16 , a skala tej jednokładności jest liczbą ujemną
Jak wyznaczyć skalę ?
27 sty 23:46
Janek191:
Napisz dobrze równanie I okręgu .
27 sty 23:49
Radek: (x−16)2+y2=4
(x−6)2+(y−4)2=16
nie chodzi o rozwiązanie, tylko jak wyznaczyć tę skalę
27 sty 23:51
Janek191:
r1 = 2
r2 = 4
więc
s = − 2
27 sty 23:54
Radek:
czemu −2 ?
27 sty 23:55
Piotr 10: bo
r2=IKI*r1
27 sty 23:56
Radek:
ale czemu nie s=2
27 sty 23:57
Piotr 10: Przeczytaj treść zadania to się dowiesz czemu s=−2
27 sty 23:58
Radek:
ale jak ją wyznaczyć ? jaki jest wzór ?
27 sty 23:58
Piotr 10: napisałem Ci wyżej
27 sty 23:59
Janek191:
O − środek jednokładności
S
1 = ( 16; 0)
S
2 = ( 6; 4)
O = ( x; y)
zatem
→ →
OS
2 = − 2* OS
1
[ 6 − x ; 4 − y ] = − 2* [ 16 − x ; 0 − y ]
[ 6 − x; 4 − y ] = [ − 32 + 2x ; 2y ]
6 − x = − 32 + 2x i 4 − y = 2y
3x = 38 3y = 4
======================
28 sty 00:02
Radek: a czemu to nie jest OS1=−2OS2
28 sty 00:09
Janek191:
Bo r2 = 2 r1
28 sty 00:10
Radek: r2 to wiekszy okrąg ?
28 sty 00:11
Janek191:
O godzinie 23.54 napisałem

wg kolejności równań okręgów

28 sty 00:15
Radek: dzięki
28 sty 00:16
Janek191:
→ oznacza wektor
28 sty 00:22
Radek:
Nie rozumiem tych przekształceń

28 sty 17:10
Radek: Czyli znowu nikt nie wytłumaczy ?
28 sty 17:17
Mila:
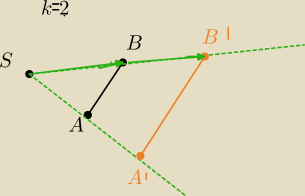
S− środek jednokładności
k=2 skala jednokładności
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k=2⇔
SA'
→=2*SA
→
SB'
→=2*SB
→
ogólnie:
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k⇔
SA'
→=k*SA
→
SB'
→=k*SB
→
28 sty 17:26
Janek191:
Których przekształceń ?
28 sty 17:26
Radek: z tymi wektorami ten zapis ?
28 sty 17:27
Radek:
Pani Milu mi chodzi o zapis tych wektorów
28 sty 17:30
Mila:
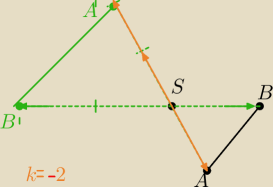
k=−2
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k=−2
Odcinki jednokładne są równoległe.
|A'B'|=|k|*|AB|
|A'B'|=2*|AB|
28 sty 17:32
Mila:
Zapis wektorów w układzie współrzędnych?
28 sty 17:33
Radek:
OS2 = − 2* OS1
[ 6 − x ; 4 − y ] = − 2* [ 16 − x ; 0 − y ]
[ 6 − x; 4 − y ] = [ − 32 + 2x ; 2y ]
6 − x = − 32 + 2x i 4 − y = 2y
dokładnie o to co wyżej
28 sty 17:34
Mila:
Wyznacz współrzędne środka jednokładności,
w której obrazem okręgu o równaniu (x−16)
2+y
2=4 , r=2
jest okrąg o równaniu (x−6 )
2+(y−4)
2 =16 , R=4
a skala tej jednokładności jest liczbą ujemną.
Okręgi są figurami jednokładnymi
k=−2 z treści ( okrąg został powiększony 2 razy)
S=(x,y) środek jednokładności
Obrazem punktu A(16,0) jest punkt A'(6,4) i to nam wystarczy do znalezienia wsp, punktu S⇔
SA'→=−2*SA→
Czy wiesz jak sie oblicza współrzędne wektora?
( od współrzędnych końca odejmujemy współrzędne początku)
SA
→=[16−x,0−y]=[16−x,−y]
SA'
→=[6−x,4−y]
Dalej rozumiesz?
28 sty 17:51
Radek: | | R | |
Tak, ale czemu |
| a nie na odwrót ? |
| | r | |
28 sty 17:57
zawodus: tak się oblicza skalę podobieństwa...
28 sty 18:08
Mila:
Promień obrazu przez promień danej figury.
28 sty 18:12
Radek:
Dziękuję zaraz wstawię zadanie ale sprawdzi ktoś ?
28 sty 18:14
zawodus: ktoś może sprawdzi...
28 sty 18:15
Mila:
Trochę więcej cierpliwości.
28 sty 18:21
Radek:
Wyznacz równanie okręgu, który jest obrazem okręgu (x+4)
2 + (y−7)
2 = 27 w jednokładności o
| | 1 | |
środku S = (− 1,4) i skali |
| |
| | 3 | |
| | 1 | |
[4−x , −7−y]= |
| [−1−x, 4−y] |
| | 3 | |
| | 1 | | 1 | | 4 | | 1 | |
[4−x, 7−y]=[− |
| − |
| x , |
| − |
| y] |
| | 3 | | 3 | | 3 | | 3 | |
12−3x=−1−x
−2x=−13
21−3y=4−y
−2y=−17
?
28 sty 18:27
zawodus: a gdzie to równanie okręgu?
28 sty 18:28
28 sty 18:29
Radek: ?
28 sty 18:34
Mila:
r=?
28 sty 18:34
28 sty 18:35
zawodus: źle
28 sty 18:37
zawodus: promień też źle...
28 sty 18:38
Janek191: r = 3

r
2 = 27 ⇒ r =
√27 = 3
√3
więc
r ' =
13 r =
√3
r'
2 = 3
28 sty 18:38

 Powinno być y' = s*y
Powinno być y' = s*y

 wg kolejności równań okręgów
wg kolejności równań okręgów 

 S− środek jednokładności
k=2 skala jednokładności
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k=2⇔
SA'→=2*SA→
SB'→=2*SB→
ogólnie:
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k⇔
SA'→=k*SA→
SB'→=k*SB→
S− środek jednokładności
k=2 skala jednokładności
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k=2⇔
SA'→=2*SA→
SB'→=2*SB→
ogólnie:
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k⇔
SA'→=k*SA→
SB'→=k*SB→
 k=−2
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k=−2
Odcinki jednokładne są równoległe.
|A'B'|=|k|*|AB|
|A'B'|=2*|AB|
k=−2
A'B' jest obrazem odcinka AB w jednokładności o środku S i skali k=−2
Odcinki jednokładne są równoległe.
|A'B'|=|k|*|AB|
|A'B'|=2*|AB|
 r2 = 27 ⇒ r = √27 = 3√3
więc
r ' = 13 r = √3
r'2 = 3
r2 = 27 ⇒ r = √27 = 3√3
więc
r ' = 13 r = √3
r'2 = 3