. icoverty: Wyznacz liczbę rozwiązań równania w zależności od parametru m

	3x+1−1
|		|=m
	3x

w mianowniku 3 też jest do potęgi x, tylko jakoś nisko jest pokazane

icoverty: można to rozwiązać w ten sposób, że rysuję sobie wykres i odczytuję wyniki tak jakby y=m ?

Aga1.:

	3x+1−1
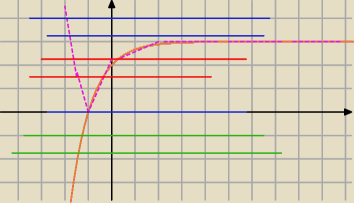
Narysuj wykres funkcji y=I		I kolor różowy
	3x

i proste y=m dla różnych m i patrz ile punktów wspólnych ma prosta z różowym wykresem.

icoverty: ok, dzięki ale czy przypadkiem x∊(−1,∞)

pigor: ..., np. tak :

	3x+1−1
|		|= m /* 3x >0 ∀x∊R ⇔ |3x+1−1|= 3x*m i m<0 , to ma 0 rozwiązań v
	3x

v |3^x+1−1|= 3^x*m i m=0 , to 3^x+1−1=0 ⇔ x+1=0 ⇔ x=−1 ma 1−dno rozwiązanie v v |3^x+1−1|= 3^xm i m>0 ⇔ (3^x+1−1=−3^xm v 3^x+1−1=3^xm) i m>0 ⇔ ⇔ (3*3^x+m*3^x=1 v 3*3^x−m*3^x=1) i m>0 ⇔ (3^x(3+m)=1 v 3^x(3−m)=1) i m>0, a więc już podsumowując widać, że : { 0 rozwiązań gdy m <0 ; g(n)= { 1 rozwiązanie gdy m=0 v m≥3 ; { 2 rozwiązania gdy 0 < m < 3 ............