Niezależność zdarzeń
Tycjan: W urnie U1 znajdują się 4 kule białe i 2 czarne, zaś w urnie U2 są 3 kule białe i 3 czarne. Z
każdej urny losujemy po jednej kuli. Oblicz prawdopodobieństwo, że wylosujemy:
a)dwie kule czarne:
b)jedną kulę czarną
c)co najmniej jedną kulę czarną,
nie wiem jak mam to policzyć, próbowałem głównie za pomocą drzewka ale wychodzą mi straszne
liczby.
Mógłby ktoś mi wytłumaczyć to na pierwszym przykładzie?
27 sty 21:43
Radek:
teraz rób

27 sty 21:45
sushi_ gg6397228:
z drzewka ładnie wychodzi, trzeba zapisac w postaci ułamka zwyklego a nie z przecinkiem
27 sty 21:45
Tycjan: Radek, P(A)=(2 1) * (3 1) ?
Nie powinno być tak?
A=(2 1) * (3 1) = 6
P(A)=6/36=1/6 − tutaj wynik się zgadza.
Teraz jednak tym sposobem nie wiem jak obliczyć b),
Sushi, coś mi to drzewko nie wychodzi, przykładowo:
a)
p=2/6 * 1/5 + 3/6 * 2/5 = 8/30 = 4/15, źle to rozpisałem ..
27 sty 21:57
sushi_ gg6397228:
skad masz 1/5 i 2/5 ?
27 sty 22:05
Tycjan:
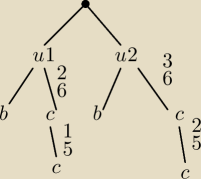
27 sty 22:11
Tycjan: Coś w tym rodzaju, to jest do podpunktu b, co ja tutaj namieszałem?
27 sty 22:11
sushi_ gg6397228:
wylosowałes po 2 kule z kazdej urny
27 sty 22:12
sushi_ gg6397228:
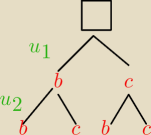
27 sty 22:14
Mila:
b)
(CB)(BC)
C) C' wylosowano dwie kule białe
|C|=36−12=24
27 sty 22:20
Radek:
a jest dobrze zrobiony ?
27 sty 22:22
PW: Radek, na litość Boską! Nie pisz takich rzeczy:
Wejdzie Ci w krew takie niechlujstwo, a potem będziesz płakał, że obcięli punkty na egzaminie.
Pierwszy napis oznacza, że Ω jest
liczbą, a drugi − że
prawdopodobieństwo jest
równe 6.
Z e r o punktów.
A gdybyś spokojnie słowami opisał czym jest przestrzeń zdarzeń elementarnych Ω, to już 1 punkt
zdobędziesz, nawet jak nie uzyskasz końcowego wyniku.
27 sty 22:22
Radek:
to jak to zapisać mam ?
27 sty 22:24
Radek:
|A|=?
27 sty 22:25
Tycjan: Sushi, "wylosowałes po 2 kule z kazdej urny", jak to? W zadaniu jest napisane, że: Z
każdej urny losujemy po jednej kuli." Co znaczy, że wylosowałem jedną kulę z jednej urny
..hmm?
27 sty 22:29
Tycjan: Dzięki Mila, zrozumiałem, mam jeszcze jedno bardzo podobne zadanie to zobaczymy czy zrozumiałem

27 sty 22:33
PW: Najpierw słowami (to naprawdę pomaga w zrozumieniu i dalszym liczeniu). Na przykład:
Ω jest zbiorem złożonym ze wszystkich możliwych dwuelementowych zbiorów {a, b}, w których a∊U
1
i b∊U
2. Wobec tego |Ω| = 6•6 = 36, gdyż w każdej z urn jest 6 kul.
Dalsze rozwiązanie musi się tego trzymać − każde zdarzenie w tym zadaniu składa się z pewnej
liczby dwuelementowych zbiorów, nie jest tym samym ważna kolejność wypisywania elementów.
Zdarzenie A − "wylosowano dwie kule czarne"
|A| = 2•3, gdyż w U
1 są dwie, a w U
2 są trzy kule czarne.
Przy takich prostych opisach nie musisz stosować tych symboli Newtona (dla mnie napis
| | | | |
| jest raczej śmieszny niż naukowy − po co strzelać z armaty do muchy?) |
| | |
27 sty 22:45
Tycjan: Po co strzelać z armaty do muchy, ależ mi to poprawiło humor.

Dzięki wielkie, nie rozumiałem
jeszcze dlaczego Zbiór Ω wynosił 36, teraz będę pamiętać, że chodzi o to ile jest kul w każdej
z urn. Jeszcze raz wielkie dzięki

27 sty 22:52
Tycjan: Jeszcze jedno pytanie w takim razie,
W urnie U1 znajduje się 6 kul białych i 4 czarne, w U2 są 3 kule białe i 7 czarnych, w U3 2
kule białe i 8 czarnych. Losujemy z każdej urny po jednej kuli. Oblicz prawdopodobieństwo, że
wylosujemy:
a)trzy kule białe,
P(A)=9/250 − wyszło pozytywnie
b)dwie kule białe, tutaj mam już jakiś problem.
Robiąc sposobem Mili nie wiem czemu mi nie wychodzi
|B|=6*3*2+4*7*8=36+224=260
P(B)=260/1000=65/250 a ma wyjść 63/250. Jakiś pomysł?
27 sty 23:02
Tycjan: hm?
27 sty 23:25
PW: Wygląda na to (po rachunkach), że u Ciebie B to zdarzenie "wylosowano po jednej kuli białej
albo po jednej kuli czarnej z każdej z urn" − wtedy byłoby 6•3•2 + 4•7•8.
Zdarzenie "wylosowano dwie kule białe" jest o wiele bardziej skomplikowane:
−dwie białe z pierwszej urny i po jednej czarnej z pozostałych lub
− dwie białe z drugiej i po jednej z pozostałych lub
− dwie białe z trzeciej i po jednej z pozostałych lub
− po jednej białej z dwóch i dokładnie jedną z trzeciej − tu są trzy możliwości..
Liczność takich zdarzeń często łatwiej ustalić poprzez zdarzenie przeciwne − w tym wypadku
B' − "wylosowano same czarne lub same białe lub jedną białą (i dwie czarne)".
27 sty 23:48




 Dzięki wielkie, nie rozumiałem
jeszcze dlaczego Zbiór Ω wynosił 36, teraz będę pamiętać, że chodzi o to ile jest kul w każdej
z urn. Jeszcze raz wielkie dzięki
Dzięki wielkie, nie rozumiałem
jeszcze dlaczego Zbiór Ω wynosił 36, teraz będę pamiętać, że chodzi o to ile jest kul w każdej
z urn. Jeszcze raz wielkie dzięki 