Walec wpisany w kule. Oblicz maksimum. HELP: Witam! Potrzebuje waszej pomocy z pilnym zadaniem. W kulę o promieniu R wpisany jest walec obrotowy. Oblicz, przy jakiej wartości promienia r podstawy walca pole jego powierzchni bocznej S osiąga maksimum.

daras: a jaki walec nie jest obrotowy

HELP: Zapewne nie ma, takie mam polecenie.

daras: to masz głupie polecenie

daras: a zrobił już jakie podejście?

HELP: Przekaże wykładowcy . Tak, rysunek narysowałem. Nie wiem nawet od czego zacząć.

daras: od Pitagorasa

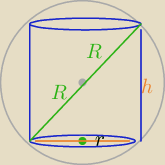
Mila: (2r)²+h²=(2R)² h=2√R²−r² S=2πrh⇔S(r)=4πr*√R²−r²

	−2r		R2−r2−r2
S'(r)=4π*(1*√R2−r2+		)=4π*
	2√R2−r2		√R2−r2

	R2−2r2
S'(r)=4π*
	√R2−r2

S'(r)=0⇔R²−2r²=0

	R2
r2=
	2

	R√2
r=
	2

	R√2
Dla r=		funkcja S(r) osiąga maksimum ( zbadaj jak zmienia się znak pochodnej Z
	2

	R√2
dodatniej na ujemną, przy przejsciu przez		)
	2

	√2R
S(		)=2πr2 przelicz.
	2

Dla ciekawości oblicz 2r i h− wniosek?

Zenek: Może mi ktoś wytłumaczyć: 1. Skąd wzięło się −2r w liczniku, dokładniej chodzi mi o samą 2.

	− 2r
2. Jak się to stało z tego (1*√R2−r2+		)
	2√R2 − r2

	R2 − r2 − r2
w to
	√R2 − r2

Mila: 1) (R²−r²)'=−2r 2) sprowadzenie do wspólnego mianownika

Zenek: Ok, ale czy w liczniku nie powinno być −2r² ? No bo r' * √R²−r² + r * (√R²−r²)' * (R²−r²)' =

	−1
= 1 * √R2−r2 + r *		* 2r =
	2√R2−r2

	−1 * r * 2r
= √R2−r2 +		=
	2√R2−r2

	−2r2
= √R2−r2 +		=
	2√R2−r2

	R2−r2−r2
=
	√R2−r2

R²−2r²=0

	R√2
r=
	2

tak?

daras: z pamięci: trza pobadać funkcję S(r) = 4πr√R² − r² , r∊(0, R), co też można zrobić w pamięci

Mila: Dobrze, Zenek, ja w pochodnej "zgubiłam r" w pierwszym zapisie obliczania pochodnej,co poprawiłeś.