.
Piotr 10: Ostrosłupy
W ostrosłupie prawidłowym czworokątnym wysokość wynosi H i tworzy z krawędzią boczną kąt 600.
Oblicz pole przekroju tego ostrosłupa płaszczyzną zawierającą przekątna podstawy i równoległej
do jednej z krawędzi bocznej.
Wydaję mi się, że przekrój ten będzie trójkątem, ale jakim ?
27 sty 18:47
Bizon:
... na pewno równoramiennym ... −

27 sty 18:53
Piotr 10: Ok, też mi tak wyszło, z mojego rozumowania
27 sty 18:54
Piotr 10: | | 2√3 | |
Wyznaczyłem podstawę tego przekroju a= |
| . ale dalej nie wiem jak wysokość przekroju |
| | 3 | |
znaleźć szukałem trójkątów podobnych
27 sty 19:05
Bizon:
...a niby dlaczego?
Podstawą jest przekątna kwadratu
27 sty 19:09
Piotr 10: | | 2H√3 | |
źle przepisałem a= |
| sorki |
| | 3 | |
27 sty 19:11
Piotr 10: ?
27 sty 19:18
Bizon:
... jak zrobisz porządny rysunek ... to zauważysz, że to specyficzny
trójkąt równoramienny ... −

27 sty 19:22
Piotr 10: właśnie mam i nic nie widzę

27 sty 19:24
Bizon:
... od środka przekątnej kwadratu podstawy prowadzisz wysokość przekroju
... leci ona pod kątem 60
o do krawędzi bocznej
A sama krawędź też jest nachylona do podstawy pod kątem 60
o
Więc jakiż to trójkąt

? −

27 sty 19:27
Piotr 10: nie rozumiem

, zapewne równoboczny
27 sty 19:30
Bizon:
... skoro nie rozumiesz .... to chyba masz zły rysunek −

27 sty 19:31
Piotr 10: dlaczego pod kątem 600 wysokość do krawędzi bocznej ?
27 sty 19:36
Bizon:
... oczywiście nie mówimy o przekroju ... a wyznaczeniu jego wysokości −

27 sty 19:38
Piotr 10: A sama krawędź też jest nachylona do podstawy pod kątem 60
0 z czego to wynika

27 sty 19:39
Bizon:
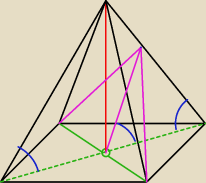
27 sty 19:43
Bizon:
... a rany
To wysokość a nie krawędż... przepraszam
27 sty 19:44
Piotr 10: nie rozumiem miara kąta(kolor niebieski) wynosi 300
27 sty 19:45
Piotr 10: jakbyś mógł mi narysować to wszystko, byłbym wdzięczny od godziny siędzę nad jednym zadaniem i
tka go nie potrafie zrobic
27 sty 19:47
Mila:
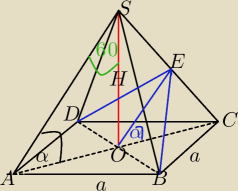
α=30
o
OE||AS
Teraz dyskutujcie.
27 sty 19:47
Piotr 10: dobra te kąy alfa rozumiem czemu są równe, próbuje dalej to zrobić
27 sty 19:49
27 sty 19:56
Piotr 10: policzyłem z tw kosinuów IOEI
IOEI=IECI=h (kąty przy podstawie te same)
IOCI
2=2h
2+h
2
?
27 sty 19:59
Piotr 10: ?
27 sty 20:19
Mila: α=30
o
Nie masz odp.? Inny mam wynik.
OE ||AS,
Z tw. Talesa
W ΔAOS:
|AO|=
√3H
|DB|=2
√3H
P
ΔDBE=
√3H
2
27 sty 20:20
Piotr 10: Policzyłem to jeszcze raz i wyszło mi tak
ΔAS0
IAOI=
√3 *H
IAOI=IOCI
ΔOEC jest równoramienny
z tw kosinusów
IOCI
2=2h
2+2h
2*0,5
3H
2=3h
2
H=h , gdzie h to wysokość w przekroju
| | 1 | | 1 | |
Pprzekroju= |
| *IDBI*H= |
| *2√3*H*H=√3H2 |
| | 2 | | 2 | |
dobrze to ? pytam się, bo te wysokości wyszły, że są sobie równe
28 sty 15:58
Mila:
Dobrze, jednak przeczytaj jak ja wyznaczyłam wysokość przekroju 20:20
28 sty 17:09
Piotr 10: OK

28 sty 17:14
Piotr 10: Mila byś mogła bardziej rozpisać swój sposób? Chodzi mi tylko o wyliczenie IOEI z Talesa ?
28 sty 17:58
Mila:
OE||AS
AS=2H
|OE|=H
28 sty 18:20
Piotr 10: Ok, dziękuję
28 sty 18:42



 ? −
? −
 , zapewne równoboczny
, zapewne równoboczny




 α=30o
OE||AS
Teraz dyskutujcie.
α=30o
OE||AS
Teraz dyskutujcie.
