jerey:

	1		2		4
jezeli zdarzenia losowe A i B: P(A)=		P(B)=		P(A∪B)=
	2		3		5

mam wyznaczyc P(A\B) jest na to jakis wzór bo w tablicach nic nie znalazłem o roznicy zdarzen losowych

Kaja: P(A/B)=P(A)−P(A∩B)

jerey: dzieki

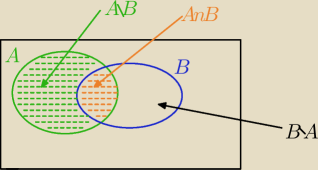
Mila: P(A\B)=P(A)−P(A∩B) ( jak przy obliczaniu pola figury) albo tak: P(AUB)=P(A\B)+P(B) dasz radę?

jerey: tak, dziekuje

jerey: a mam jeszcze pytanie , nie dotyczace prawdopodboienstwa ale permutacji. jezeli w kolejce do kasy biletowej ustawiły sie 4 dziewczynki i 5 chlopcow to liczba wszystkich ustawien: 4!*5! czy bierzemy ogłem wszystkich pod uwagę nie zważając na kolenosc ustawienia (chodzi mi o to ze mozemy mieszać chłopców z dziewczynkami naprzemiennie) i założyc ze mozliwych jest 9! ustawien. Jednak z warunkow zadania: mamy podaną kolejnosc; najpierw ustawiły sie 4 dziewczynki czyli 4! sposoby nastepnie chlopcy 5! sposobów. Zadanie jest podchwytliwe i w koncu zdurniałem. Mila mozesz mi to wytłumaczyć?

Kaja: nie pisze że dziewczynki stoją przed chłopcami, więc bierzemy ogółem wszystkich pod uwagę.

jerey: czyli mozliwych ustawien jest 9!?

Kaja: tak

Mila: Napisz dokładnie treść. WAŻNE!

jerey: juz jest w porządku, zle zrozumiałem zadanie po prostu. W kolejce do kasy biletowej ustawiły się 4 dziewczynki i 5 chłopców. Liczba wszystkich mozliwych ustawien osób w tej kolejce wynosi

Mila: 9!