Obliczyć całke podwójna Piotrek22: Obliczyć całkę podwójna ∬(x² + 2y)dxdy gdzie obszar calkowania D ograniczony jest prostymi y = 2x , x = 3 i hiperbola y = 1/2x opisac ten opszar mi wyszly dwa obszary całkowania D1 = 1/2x ≤ x ≤ 3 1/2x ≤ x ≤ 1 D2 = 2x ≤ x ≤ 3 1 ≤ y ≤ 2x to jest dobrze pomoze ktos

wredulus_pospolitus: jak obszar 'x' może być ograniczony przez 'x'

1
	x ≤ x <−−− co to w ogóle oznacza
2

granice całkowania względem jednej zmiennej mają być zależne od drugiej ... ale juz granice całkowania tej drugiej zmiennej musza być 'jawne' (czyli granicami mają być konkretne liczby)

Piotrek22: 1 −−− nie umiem robic w tym programie ulamków to mialem na mysli 1/2x 2x

Piotrek22: 1 −−− 2x

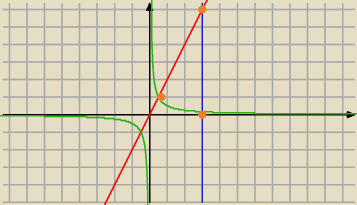
wredulus_pospolitus: (punkt przecięcia się hiperboli i prostej) ≤ x ≤ 3 hiperbola ≤ y ≤ prosta takie granice całkowania mogą być

Piotrek22: to wtedy na x beda 1≤x≤3 ? tak moze byc

Piotrek22:

	1
		≤ y ≤ 2x
	2x

wredulus_pospolitus: no raczej na pewno nie '1' bo przez punkt (1,1) nie przechodzi prosta y=2x

Piotrek22:

	1
z mojego rysunku przecina sie y= 2x z parabola w punkcie		≤ x ≤ 3
	2

wredulus_pospolitus: i to juz lepiej ale lepiej nie odczytywać 'z rysunku' a obliczyć ... wyznaczyć punkt przecięcia algebraicznie

Piotrek22: dzieki teraz trzeba obliczyć całke podwójna podstawiajac za x i za y granice calkowania