Obliczyć pole ograniczona parabola Piotrek22: Obliczyć pole ograniczona parabola y² = 4 + x i prosta x + 3y = 0 Wykonać rysunek

wredulus_pospolitus: rysunek wykonałeś

wredulus_pospolitus: punkty przecięcia wyliczyłeś

wredulus_pospolitus: całke oznaczoną zapisałeś

wredulus_pospolitus: a ją obliczyłeś

wredulus_pospolitus: nie no to teraz juz wiesz co po kolei masz zrobić

Piotrek22: rysunek wychodzi dziwny punkty przeciecia sa dziwne zrobilem parabole x=y²−4 i prosta x=−3y tak mozna ?

Piotrek22: wyszlo mi opszar calkowania y²−4 ≤ x ≤0 i 0 ≤ y ≤−3y

wredulus_pospolitus: całka podwójna co to za obszary całkowania jakie punkty przecięcia Ci wyszły

Piotrek22: do tego sa to dwa obszary trzeba było by razy dwa chyba ze pomylilem sie co do wykonania rysunku

Piotrek22: nom to bedzie całka podwójna

Piotrek22: dobry mam obszar calkowania ?

wredulus_pospolitus: nie będzie żadna całka podwójna całka podwójna służy do liczenia OBJĘTOŚCI pod powierzchnią (czyli liczona jest w R³ bądź wyżej) to będzie zwykła całka pojedyncza ... pytanie brzmi ... czy jestes w stanie wyznaczyć punkty przecięcia się tych dwóch krzywych

Piotrek22: narysowalem parabole x=y² − 4 i przechodzi w punktach na osia x −2,2 oraz na osia y w punkcie −4 a prosta x=3y przechodzi przez srodek czyli 0,0

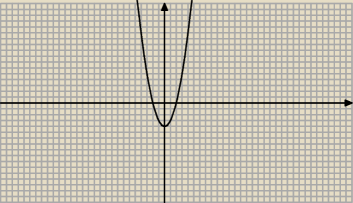
5-latek: To co napisales to byla by taka parabola y=x²−4

Piotrek22: zgadzam sie i do tego prosta x = −3y przechodzi ona w punkcie 0,0

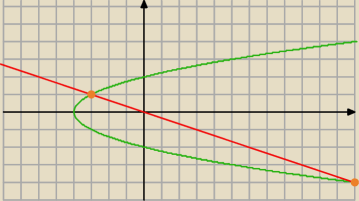
wredulus_pospolitus: ale Ty takiej paraboli nie masz ... to raz a dwa ... nadal nie podałeś punktów przecięcia

wredulus_pospolitus:

Piotrek22: pierwszy punkt to A(−3,1) B(0,0) C(0,2) tak ?

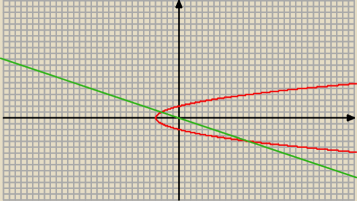
Janek191: y² = 4 + x ⇒ y = √ x + 4 lub y = − √x + 4

	x
x + 3y = 0 ⇒ y = −
	3

Szukam punktów wspólnych prostej i paraboli: y² = 4 + x

	x
y = −
	3

−−−−−−−

x2
	= x + 4
9

x² = 9x + 36 x² − 9 x − 36 = 0 Δ = 225 √Δ = 15 x₁ = − 3 x₂ = 12 Pole P = P₁ + P₂ , gdzie P₁ − pole nad osią OX, P₂ − pole pod osią OX

5-latek: Piotrek przeciez masz na rysnku ze beda 2 punkty przecia tej parabli z prosta a nie 3 . A potrafisz to wyznaczyc algebraicznie ?

Janek191: y² = 4 + x ⇒ y = √ x + 4 lub y = − √x + 4

	x
x + 3y = 0 ⇒ y = −
	3

Szukam punktów wspólnych prostej i paraboli: y² = 4 + x

	x
y = −
	3

−−−−−−−

x2
	= x + 4
9

x² = 9x + 36 x² − 9 x − 36 = 0 Δ = 225 √Δ = 15 x₁ = − 3 x₂ = 12 Pole P = P₁ + P₂ , gdzie P₁ − pole nad osią OX, P₂ − pole pod osią OX

Janek191: y² = 4 + x ⇒ y = √ x + 4 lub y = − √x + 4

	x
x + 3y = 0 ⇒ y = −
	3

Szukam punktów wspólnych prostej i paraboli: y² = 4 + x

	x
y = −
	3

−−−−−−−

x2
	= x + 4
9

x² = 9x + 36 x² − 9 x − 36 = 0 Δ = 225 √Δ = 15 x₁ = − 3 x₂ = 12 Pole P = P₁ + P₂ , gdzie P₁ − pole nad osią OX, P₂ − pole pod osią OX

Piotrek22: no i jak mam punkty przeciecia sie z osia x to co dalej ? bo juz kompletnie nic nie kumam pod co musze to podstawic aby obliczyć te pole zrobic calke pojedyncza z √x + 4

wredulus_pospolitus: skoro 'nie kumasz' to ja się Ciebie zapytam ... co robileś na ćwiczeniach w końcu całki masz nie od wczoraj (skoro masz całki podwójne także)

Piotrek22: wiesz studia zaoczne nie oferuja duzo godzin cwiczen a raczej przedstawienie teorii i materiału do nauki wiem sa braki w podstawach

zawodus: jest pełno pdf−ów z przykładami na necie i można się samemu nauczyć − jeśli się chce

Piotrek22: zgadzam sie z tym ale trzeba miec czas praca i inne sprawy itd pochłaniają czas ale dzieki za pomoc

Piotrek22: ponawiam pytanie jak juz znam miejsce przecięcia sie tych puntów co dalej trzeba zrobic? jak teraz zapisać całke oznaczona ?