Geometria analityczna Sugi: Znajdź równanie okręgu wiedząć że jego środek należy do prostej o równaniu x−y=0, jest on styczny do prostej k: y−5=0 i przechodzi przez środek okręgu o równaniu x²+y²−8x−2y+1=0 nie potrafie wgl tego zrobić proszę o pomoc muszę mieć to na 8 rano zrobione ;c

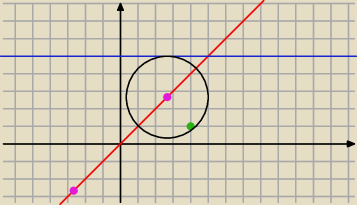
ICSP: równanie okręgu : (x− x_s)² + (y −y_s)² = r² gdzie (x_s;y_s) − współrzędne środka, r − promień środek należy do prostej y = x zatem y_s = x_s wstawiając do równania mamy : (x− x_s)² + (y −x_s)² = r² Okrąg jest styczny do prostej y= 5 zatem r = 5 − x_s Wstawiając do równania okręgu mamy : (x− x_s)² + (y −x_s)² = (5 − x_s)² Wyznaczmy teraz współrzędne środa drugiego okręgu : x² + y² − 8x− 2y + 1 = 0 x² −8x + 16 + y² − 2y + 1 = 16 + 1 − 1 (x−4)² + (y−1)² = 4² S₁(4 ; 1) Punkt S₁ należy do pierwszego okręgu. Podstawiając za x 4 oraz za y 2 dostajemy : (4 − x_s)² + (1 − x_s)² = (5 − x_s)² 16− 8x_s + x_s² + 1 − 2x_s + x_s² = 25 − 10x_s + x_s² x_s² −9 = 0 x_s = 2√2 x_s = −2√2 Zatem mamy dwa okręgi spełniające warunki zadania : (x − 2√2)² + (y −2√2)² = (5 − 2√2)² (x + 2√2)² + (y +2√2)² = (5 + 2√2)²

5-latek: Mialo byc na godzine 8 rano wiec dziekuje Ci ICSP