Bok AB trójkąta ABC ma długość równą c. Punkty K, L, M są środkami odpowiednio b Zosia: Bok AB trójkąta ABC ma długość równą c. Punkty K, L, M są środkami odpowiednio boków AB, BC, AC. Wyznacz długość wektora u. a) wektor u →=KL→ + KA→ − MC→ b) u→ = KB→ + LC→ + MA→ Ad. a) czy dobrze rozumiem u→ wyznaczony za pomocą zmiennej c jak długości czy c→ ?

	1
KL→= KB→ + BL→ ⇒ KL→ =		c + BL→
	2

	1
KA→ = KM→ + MA→ ⇒		c→ = KM→ + MA →
	2

MC→ = CA→ − AM→

pigor: ...., nie będę używał → , bo wiadomo o co chodzi a) wektory u=KL+KA−MC=KL+LM+CM=KL+LM+MA=KA ⇒ |u|= |KA|= ¹₂c, lub inaczej, jeśli O − wektor zerowy, to a) u=KL+KA−MC= KA+KL−MC= KA+O=KA i dalej jak wyżej bo wektor KL||MC i |KL|=|MC| równe i przeciwnie skierowane. −−−−−−−−−−−−−−−−−−−−−−−−−−−−− analogicznie w b) u=KB+LC+MA=KB+BL+LK=O ⇒ |u|=|O|=0, czyli długość równa zero.

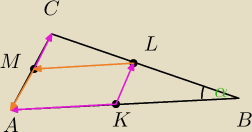
Mati_gg9225535: z rysunku wynika ze w a) długosc wektora u jest rowna 0 wystarczy wykazac ze trojkaty ZBC i KBL są podobne, z twierdzenia talesa albo cecha bok kąt bok (bkb) i na mocy podobienstwa stwierdzamy ze AC || KL więc wektor KA = wektor LM i dopisać że MA = −MC

Mati_gg9225535: racja pigor w a) wektor u = 1/2 c

pigor: ..., masz na myśli długość wektora u, czyli |u|= ¹₂c, ... prawda