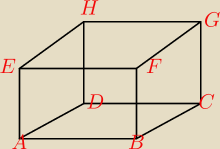
jerey: w worku znajduje sie osiem piłeczek pingpongowych oznaczonych literami od A−H, odpowiadającymi wierzchołkom szescianu. Bolek lusuje kolejno trzy piłeczki. Oblicz prawdopodobienstwo zdarzenia ze litery na wylosowanych piłeczkach odpowiadają wierzchołkom trojkąta rownobocznego. 1−8→A−H Ω=8

	8 3
bolek moze wylosowac 3 piłki na		czyli 56 sposobów.

w szescianie mozna utworzyc 8 trojkątow rownobocznych ? po przekątnych. ; mozliwosci to: DBC BDE HFA HFC EGD EGB ACH ACF doszedłem do tego i nie wiem jak dalej ruszyc to zadanie, kiepsko mi idzie prawdopodobienstwo i kombinatoryka. podsuniecie mi jakies pomysły?

jerey: DBG*

jerey: Ω=8*7*6 ***

jerey: odswiezam

PW: No nie żartuj, masz liczność przestrzeni zdarzeń Ω i masz liczność zdarzenia A (o które pytają). Twierdzenie zwane klasyczną definicją prawdopodobieństwa, czyli to najłatwiejsze, co wszyscy kojarzą.

zawodus: Zastanów się czy kolejność rozróżniasz czy nie... bo wynik ten sam ale liczy się inaczej... Raz piszesz tak a raz tak (chodzi o omegę)

PW: O licho, teraz zmieniłeś zdanie co do liczności Ω? Starzy nauczyciele mają rację: po pierwsze napisz wyraźnie co jest w tym zadaniu zdarzeniem elementarnym − zapisz Ω w postaci wzoru lub (łatwiej) opisu słownego.