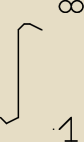
taka tam całeczka ... MarcoPolo: oznaczona nie policzona hmmm jakaś podpowiedź... mam całkę :

	1		1
∫ (oo 1)		e {		} dx
	x3		x

MarcoPolo:

	1
e ma do kwadratu		coś mi nie chciało poprawnie zapisać równania
	x

Kejt:

	1
∫		*e1/xdx?
	x3

MarcoPolo: tak

Kejt: przez części

	1
całka z		i pochodna z e1/x i do skutku.
	x3

powinno pójść.. trzeba po prostu zmniejszyć potęgę przy x do zera.

Kejt: jak nie dasz rady to wrzucę rozwiązanie..

MarcoPolo: dobra juz się zabieram do rozwiązywania dzięki, zaraz wynik pokaże

Kejt: czekaj, znalazłam błąd w rozumowaniu.. zaraz pomyślę..

MarcoPolo: hmm zobacz: nieoznaczona na początek

	1		1
∫		e1/x= | f(x)=e1/x −−−−> f'(x)=		e1/x
	x3		x

	1
|g'(x)=x−3 −−−−−>g(x)= −		x−2
	2

	1		1
=U{1}[2}x−2*e1/x − ∫		x−2 =		x−2*e1/x ... i teraz za e1/x pochodną a U{1}[x}
	x		2

całkę ?

MarcoPolo: kurczę za szybko pisałem i nie te nawiasy przepraszam ale chyba wiadomo ocb ...

MarcoPolo:

	1
a i teraz jak za		wezmę całkowanie to wyjdzie x0 ?
	x

Kejt: problem w tym, że ta potęga wraca przy e.. zrobiłam podstawienie, ale utknęłam na całce: ∫e^1/xdx.. wstyd się przyznać

ICSP:

	1
ja bym zaczął całą całkę od podstawienia t=
	x

	−1
wtedy dt =		dx
	x2

1		1		1
	=		*
x3		x		x2

Kejt: dobra.. już widzę.. podstawienie miałam takie samo, ale potem nagle zamiast t=1/x zrobiło się t=x.. wychodzi: −∫t*e^tdt

MarcoPolo:

	t
no to całka miała by postać ∫		* et ?
	x2

Kejt: nie możesz mieć jednocześnie x i t w jednej całce..

MarcoPolo:

	1
∫ t*		*et ?
	x2

Kejt: nie.

	1
t=
	x

	1
dt=−		dx
	x2

zatem −∫t*e^tdt

MarcoPolo: tylko jak dalej to rozwiązać bo już nie wiem /

Kejt: przez części: u=t v'=e^t u'=1 v=e^t =−(t*e^t−∫e^tdt)=−(t*e^t−e^t)+C=...

MarcoPolo: dzieki