wielokaty zadanie: 1. Dany jest 15−kat foremny A1A2A3 ...A15. Dla podanych x, y, z, s wskazac takie t, ze pieciokat wypukły o wierzchołkach Ax, Ay, Az, As, At (niekoniecznie lezacych na obwodzie pieciokata w tej kolejnosci) ma pole równe polu pieciokata A1A3A6A10A15. a) x=1, y =4, z =5, s=7, t= ......................... ; b) x=1, y =4, z =8, s=11, t= ......................... ; c) x=1, y =6, z =11, s=12, t= ......................... ; d) x=1, y =6, z =11, s=13, t= ......................... . moze cos z tymi indeksami ? prosilbym o pomoc?

zadanie: ?

zadanie: bo odp. sa takie: a) t= 11 lub 12 ; b) t= 2 lub 3 lub 9 lub 10 ; c) t= 3 lub 4 lub 8 lub 9 ; d) t= 2 lub 5 lub 7 lub 10 ale ja nie wiem jak do tego dojsc moze jakies roznice indeksow?

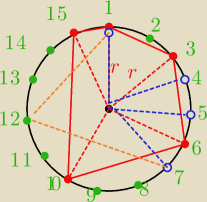
Mila: źle tam policzyłam pole. α=24^o

	1
P A1A3A6A10A15=		r2*(sinα+sin(2*α)+sin(3*α)+sin(4*α)+sin(5*α))
	2

Dobrze ,że dałes odpowiedzi. a) x=1, y =4, z =5, s=7, t= zostało 9 kątów środkowych

	1
Pa=		r2*((sin3α+sin(α)+sin(2*α)+sin(k*α)+sin((9−k)*α))
	2

sin(k*α)+sin((9−k)*α)=sin(4*α)+sin(5*α)

	kα+(9−k)α		kα−(9−k)α		9		−α
2 sin		*cos		=2 sin		α*cos
	2		2		2		2

	9		kα−(9−k)α		9		−α
sin		α*cos		=sin		α*cos
	2		2		2		2

kα−(9−k)α		−α
	=
2		2

2kα−9α=−α 2k−9=−1 2k=8 k=4 dodajemy 4 katy środkowe począwszy od W₇ W₇+4=W₁₁⇔t=11 albo 4 kąty srodkowe w lewo od W₁ W₁−4=W₁₂ ⇔t=12 posprawdzaj zapisy, bo moga być literówki.

zadanie: dziekuje

Mila: Mam nadzieję, że bez liczenia ustaliłeś.

Mila: W podanym pięciokącie kąty środkowe: 2α,3α,4α,5α,1α b)1,4,8,11 Masz kąty środkowe: 3α, 4α,3α od W11do W1 masz 5α, jeden z kątów 3α dzielisz na kąty 1α,2α Zatem po kolei, dzielisz kąt między W1 i W4 masz 2 warianty W1,W2,W4,W8,W11, albo W1,W3,W4,W8,W11 dzielisz kąt między W8 i W11 i masz dwa warianty W1,W4,W8,W9,W11 albo W1,W4,W8,W10,W11