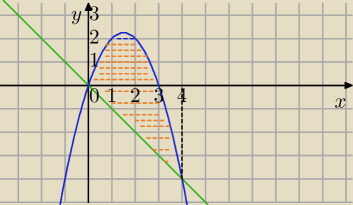
Całka oznaczona cbk: Oblicz pole figury ograniczonej liniami. Chodzi i całkę oznaczoną. a) y = 5x² − 6x , y=0 , x= −1 , x= 1 Tu mi wyszło równe 6 b) y = 3x − x² , y = −x Tego nie wiem jak zacząć. Liczyć dwa pola oddzielnie? ale wtedy to pod osią Y jest ograniczone trzema liniami. A jak jako jedno pole to gdzie trzeba wrzucić minus, który się wstawia przed całkę gdy pole jest pod osią?

PW: b) Dlaczego trzema liniami? Parabolą i prostą y=−x. Miejsca zerowe paraboli to 0 i 3, a więc na przedziale [0, 3] całkujemy różnicę (3x−x²) − (−x) (uzyskamy pole pod parabolą i nad prostą), a na przedziale [3, 4] wykresy obu funkcji leżą pod osią − wymyśl.

cbk: Noo tak, leżą i policzyłem to ale pole mi wyszło na minusie. A na przedziale [0,3] nic nie szkodzi, że kawałek pola tej figury leży pod osią Y i nie trzeba wstawiać minusa?

Mila: 3x−x²=−x 4x−x²=0 x(4−x)=0 x=0 lub x=4

	1		64		32
0∫4(3x−x2−(−x))dx=0∫4(4x−x2)dx=[ 2x2−		x3]04=32−		=
	3		3		3

cbk: Dokładnie tak zrobiłem. I mi tak samo wyszło, ale to, że kawałek pola leży pod osią nie ma znaczenia? Nie wstawia się nigdzie minusa?

Mila: Nie.

cbk: To kiedy należy wstawić minus przed całkę?

PW: Miałeś wymyślić, a się dopytujesz. To proste − zobacz "interpretacja geometryczna całki oznaczonej" czy jakoś tak

cbk: Jeśli nie wymyśliłem to che się dowiedzieć.