Prawdopodobnieństwo chiara: W urnie było n białych i 2 czarne kule. Wyjęto jedną kulę i przełożono do drugiej urny, w której było początkowo 5 białych i 3 czarne kule. Z drugiej urny wyjęto teraz jedną kulę. Oblicz liczbę n jeśli wiadomo, że prawdopodobieństwo wylosowania z drugiej urny kuli białej jest równe ¹⁷₂₅

chiara: proszę o dokładne wytłumaczenie

wredulus_pospolitus: rozpatrujemy dwa przypadki: 1) wylosowano w pierwszej białą i w drugiej białą:

	n		6
P('1') =		*
	n+2		10

2) wylosowano w pierwszej czarną, a w drugiej białą:

	2		5
P('2') =		*
	n+2		10

	17
dodaj do siebie te dwa przypadki ... ich suma =
	2...cos tam masz...

wyznacz 'n'

chiara: ale po obliczeniu w ten sposób n wyszło ujemne...

chiara: czy ktoś może mi powiedzieć jak to powinno się zrobić?

Mila: 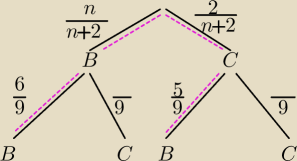Masz błąd w danych

	17
ma być
	27

II urna :6 B,3C Jeśli z U₁ wylosowano białą kulę II urna :5 B,4C Jeśli z U₁ wylosowano białą czarną

	n		6		2		5
P(B)=		*		+		*
	n+2		9		n+2		9

n		6		2		5		17
	*		+		*		=
n+2		9		n+2		9		27

6n+10		17
	=		⇔
9(n+2)		27

27(6n+10)=17*9(n+2) /:9 3(6n+10)=17(n+2) 18n+30=17n+34 n=4