PUNKT PRZEGIĘCIA I WYPUKŁOŚĆ
Klaudia18: PUNKT PRZEGIĘCIA I WYPUKŁOŚĆ
f(x)= ln2x+ 2lnx
25 sty 14:14
Klaudia18: | | 1 | |
f'(x)= 2ln * |
| + U{2}[x} |
| | x | |
25 sty 14:28
25 sty 14:29
Klaudia18: pomoże ktoś ?
25 sty 15:05
piter: Obliczasz druga pochodna z tego i przyrownujesz do 0.
25 sty 15:13
Klaudia18: | | 2 | | 1 | |
no dobra to 2 pochodna tego to |
| +2lnx(− |
| ) ? możę ktoś sprawdzić bo nie |
| | x2 | | x2 | |
wychodzi mi dalej dlatego pytam?
25 sty 15:17
Nina123: ponawiam pytanie... wytłumaczy ktoś ?
25 sty 20:47
Kejt: w czym problem?
25 sty 20:56
b.: | | 2 | |
w drugiej pochodnej zgubiłaś jeden składnik: chyba nie zróżniczkowałaś |
| |
| | x | |
25 sty 20:59
daras: wypukła do dołu czy do góry?
bo co autor to inna wersja
25 sty 21:20
Nina123: od nowa napiszę i proszę o sprawdzenie:
f(x)= ln
2 x + 2lnx
| | 2lnx | | 2 | | 2lnx+2 | |
f'(X)= |
| + |
| = |
| |
| | x | | x | | x | |
| | 2lnx+2)'*x−(2lnx+2)*(x)' | |
f''(x)= |
| = |
| | x2 | |
| | 2−(2ln+2) | |
= |
| ... i co dalej muszę zrobić aby ten punkt przegięcia i wypukłość |
| | x2 | |
zrobić
wiem że od 2 pochodnej zależy czy będzie wypukła ku dołowi czy wypukła ku górze ... i mam
problem określić to po 2 pochodnej ....
25 sty 21:26
Kejt: na początek skróć te dwójki w liczniku

25 sty 21:36
wredulus:
Okresl znak drugiej pochodnej (analogicznie do monotoncznosci okreslanej z pierwszej pochodnej)
25 sty 21:37
wredulus: No i oczywiscie −−− gdzie jest napisana dziedzina funkcji oraz jej pochodnych

25 sty 21:38
Kejt: a potem:
2lnx=0
lnx=0
lnx=ln1
x=1
i zaraz zrobię do tego rysunek..
25 sty 21:38
Nina123: czyli tak skracam 2 i mnoże przez mianownik i mam −2lnx=0
no to 2 pochodna wychodzi że jest ujemna
25 sty 21:40
Nina123: aha lnx=ln1 ponieważ lnx=0 a ln1=0 z tego to wynika ... i jest x=1
25 sty 21:42
Kejt:
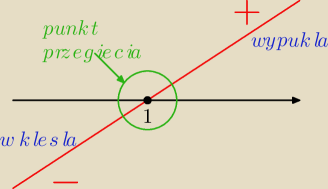
25 sty 21:44
Nina123: punkt przegięcia to x=1 a rodzaj wypukłości jak sformułować w odpowiedzi?
że od (−oo,1) jest wklęsła a w przedziale (1,+oo) jest wypukła ?
25 sty 21:50
wredulus:
Nina ... jeszcze raz napisze −−−− jaka jest dziedzina funkcji

25 sty 21:51
Kejt: tak, tak jak napisałaś.
25 sty 21:51
Nina123: no dziedzina z ln to będzie
D: x> (bądź rowne) 0
25 sty 21:53
Kejt: ≠0
25 sty 21:54
Nina123: dziękuje

25 sty 21:57




