Funkcje - ekstrema Maja: Znaleźć ekstrema funkcji i równania asymtot odpowiadających im krzywych. y= w liczniku x²−3x+2/w mianowniku x²+3x+2

zośka:

	x2−3x+2		x2−3x+2
y=		=
	x2+3x+2		(x+1)(x+2)

zatem D_f=R\{−1,−2} Policz teraz pierwszą pochodną

Maja: to już mam, co dalej?, bo ja kompletnie zapomniałam już to, 30 lat po maturze:(

Maja: licznik pochodnej mam już 6x² − 12, a mianownik w polu

zośka: Przyrównaj pochodną do zera. Otrzymasz miejsca gdzie może występować ekstremum

zośka:

	6(x−√2)(x+√2)
y'=
	(x+1)2(x+3)2

D_f'=D_f y'=0 ⇔x=√2 lub x=−√2 Teraz trzeba narysować wężyk i zbadać jak zmienia się znak pochodnej

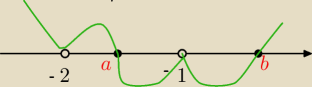
zośka: Tam w mianowniku zamiast 3 oczywiście . a=−√2 b=√2

zośka: w a pochodna zmienia znak z + na − , więc w tym miejscu jest maximum w b masz minimum

Maja: Dzięki bardzo Zosia