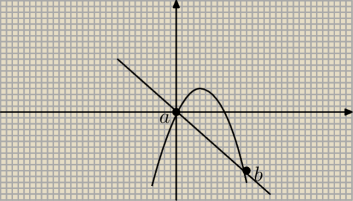
Całka oznaczona Renn: Mam obliczyć pole figury ograniczone wykresami fkcji: x+y=0 oraz y=2x−x² Narysowałam sobie wykres i muszę wyznaczyć granice całkowania (pkty a i b na rysunku) z zależności: −x=2x−x² (to z tych dwóch powyższych równań) − i nie mam problemu z całką, tylko właśnie z tym dziadostwem...

zośka: W czym problem? 0=3x−x² 0=x(3−x) x=0 lub x=3 y=0 y=−3 granice więc bedziesz mieć od 0 do 3

5-latek: x²−2x−x=0 to x²−3x=0 to x(x−3)=0 to x=0 lub x−3=0 to x=3 mysle ze tak

zośka: I najpierw całka z f. kwadratowej −całka z f.liniowej

zośka:

	3x2		x3
∫(2x−x2)dx − ∫(−x)dx=∫(3x−x2)dx=[		−		]
	2		3

To w granicach od 0 d0 3 wychodzi chyba 4,5