. Piotr: W czworokącie wypukłym ABCD dane są kąty:

	DB		√2
I∡ADCI=I∡ABCI=900 oraz I∡DCBI=1350. Wykaż, że		=
	AC		2

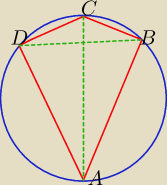
W zadaniu nie miałem okręgu, ale narysowałem sobie go: Czworokąt jest wpisany w okrąg, bo I∡AI=360⁰ − (180⁰ +135⁰)=45⁰ Suma przeciwległych kątów jest równa 180⁰. IACI=2*R, gdzie R− promień okręgu opisanego na czworokącie ΔDBA (tw. sinusów)

DB
	=2*R
sin450

	√2
IDBI=2*R*
	2

Jest dobrze ?

Piotr 10: ?

Eta: ok ale Dopisz bardziej szczegółowy komentarz , że |AC|=2R ( dlaczego?) i że okrąg opisany na czworokącie jest również opisany na trójkącie ABD

	|DB|
dlatego		= 2R
	sin45o

Piotr 10: Dlatego, że odcinek IACI przechodzi przez środek okręgu, a punkty A i C znajdują się na okręgu, tak ?

5-latek: Piotr a ile wynosi kat wpisany oparty na srednicy?

Piotr 10: 90⁰ ok nie było pytania, dzięki