Ciągi matematykaa: Zbadaj monotoniczność ciągu określonego wzorem a_n=(−n+2)³ błaaagam

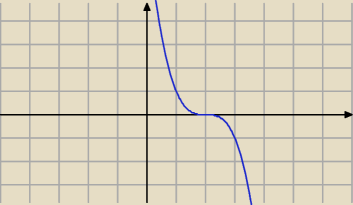
Mila: Funkcja f(x)=x³ funkcja rosnąca Funkcja f(x)=(−x+2)³ jest funkcją malejącą dla x∊R, zatem ciąg jako f(n)=(−n+2)³ też jest malejący dla neN₊

5-latek:

	an+1
an+1−an lub		i licz
	an

PW: O taką prostą rzecz aż błaganie? Rutynowo bada się różnicę a_k+1−a_k= (−k−1+2)³ − (−k+2)³ = (−k+1)³ − (−k+2)³ starając się pokazać że jest ona dodatnia albo ujemna dla wszystkich k − wtedy ciąg jest rosnący albo malejący. Spróbuj − to głupie rachunki.

matematykaa: wychodzi mi −3n²+9n−7<0 i co z tym

Mila: Δ=81−4*(−3)*(−7)=81−84<0 Parabola skierowana w dół, brak miejsc zerowych, trójmian przyjmuje tylko wartości ujemne, ciąg malejący.

PW: Okazuje się że rachunki były łatwe, tylko wnioski trudne. Ćwicz dalej, matematykoo.

Mila: Zapomniała nam podziękować.