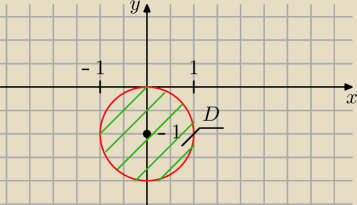
Obliczyć całkę podwójną. Rude: ∫∫(x*sin(y) − y)dxdy, D=x²+y²+2y <= 0 będę bardzo wdzięczna za pomoc!

asdf: czego nie wiesz?

Rude: zamieniam x, y, na zmienne biegunowe. okrąg, który jest obszarem jest przesunięty i dochodzę do: ∫{od 0 do 2π} [ ∫ {od 0 do −2sinφ} rcosφ*sin(rsinφ)−rsinφrdr]dφ i nie mam żadnego pomysłu jak to policzyć. (zakładając, ze nie zrobiłam błędu gdzieś wcześniej)

Trivial: Całkę można rozbić na dwie części. α = ∬Dxsin(y) dxdy = ∫−2−1dy ∫−√1−(y+1)2+√1−(y+1)2xsin(y) dx = ∫−2−1[12x2sin(y)]x=−√1−(y+1)2x=+√1−(y+1)2 dy = 0. W drugiej części stosujemy podstawienie

	⎧	x = rcosφ
	⎩	y = rsinφ − 1

β = −∬_Dy dxdy = −∬_G(rsinφ − 1) rdrdφ = −∬_Gr²sinφ drdφ + ∬_Gr drdφ = ∫₀¹r² dr*∫₀^2π(−sinφ) dφ + ¹₂*2π = π A zatem ∬_D (xsin(y) − y) dxdy = α + β = π. I sprawdzenie: http://www.wolframalpha.com/input/?i=Integrate[x*sin%28y%29+-+y%2C+{+x%2C+-1%2C+1}%2C+{y%2C+-1+-+sqrt%281-x^2%29%2C-1+%2B+sqrt%281-x^2%29}]

Rude: dzięki wielkie za szybką i zrozumiałą odpowiedź.