Równanie z parametrem chiara: Dla jakich wartości parametru k równanie x² + 2( k − 3)x + 9 = 0 ma dwa różne pierwiastki x1 i x2 spełniające nierówności: − 6 < x1 < 1 i −6 < x2 < 1? Wiem, że początek to Δ>0 i z tego wychodzi, że k∊ (−∞, 0) ∪ (6, +∞) ale nie wiem, jak rozwiązać dalej te nierówności. Proszę o dokładne wytłumaczenie.

kika: −12<x₁+x₂<2 i wzory Viete'a −12<−2(k+3)<2 −6<−2k<7

chiara: a skąd taka zależność?

J: Tutaj jest drobna pomyłka: −12<−2(k+3)<2 ⇔ −12<−2k<8

ZKS: kika według mnie nie można tak zrobić. Z tego co napisałaś biorąc część wspólna z warunkiem Δ > 0 otrzymujemy sprzeczność natomiast dla k = 6.5 dostajemy pierwiastki znajdujące się w danym przedziale. U Ciebie łatwo pokazać że to co napisałaś nie jest prawdą biorąc przykładowo za x₁ = −7 a za x₂ = −4 po sumowaniu x₁ + x₂ = −11 i według Twojego zapisu −12 < x₁ + x₂ < 2 znajduje się w przedziale ta −11 natomiast osobno już x₁ nie należy do przedziału (−6 ; 1). Mam nadzieję że w zrozumiały sposób wyjaśniłem błąd.

Piotr 10: 1⁰ Δ > 0 2⁰ − 6 < x₁ < 1 −6 < x₂ < 1 dodając to stronami: −12 < x₁+x₂ < 2 : 2 −6 < x_w < 1

J: Podzielam opinię "ZKS".To że suma dwóch liczb należy do przedziału (−12;2) nie oznacza ,że każda z nich nalezy do przedziału (−6;1), co w prosty sposób wykazał

ZKS: 1^o Δ > 0 2^o x_w ∊ (−6 ; 1) 3^o f(1) > 0 4^o f(−6) > 0.

J: I to ma sens

ZKS:

chiara: ale skąd się własnie wzięły 2,3 i 4 przypadek, bo właśnie tego nie rozumiem. mógłby ktoś to jakoś jasno wytłumaczyć?

J: Ad2^o) Gdyby wierzchołek paraboli leżał poza przedziałem (−6;1) to obydwa pierwiastki nie mogłyby należeć do przedziału (−6;1) Ad 3^o i 4^o ) gwarantują,że oba pierwiastki należą do przedziału (−6;1) , bo jeżeli f(1)>0 to oznacza, że f(x<1) ≤ 0 i podobnie jeżeli f(−6)>0 to oznacza,że f(x>−6)≤0

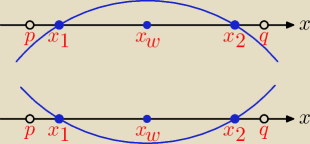
Bogdan: Podaję założenia do:

	−b
ax2 + bx + c = 0, x1∊(p, q) i x2∊(x1, x2), xw =
	2a

(1) a≠0 (2) Δ>0 (3) af(p)>0 (4) af(q)>0

	−b
(5)		>p
	2a

	−b
(6)		<q
	2a

Rozwiązaniem jest część wspólna rozwiązań podanych nierówności/ W tym zadaniu p=−6, q=1

chiara: dziękuję bardzo