Jak obliczyć największą i najmniejszą wartość funkcji kwadratowej? małami: Jak obliczyć najmniejszą i największą wartość funkcji kwadratowej bez obliczania delty? Przykład: f(x) = ¹₂x² − 4, Df = <−1, 4> Ramiona paraboli skierowane są do góry, więc największą wartość można łatwo obliczyć − wynosi 4. A co z najmniejszą wartością?

Bogdan: Podaj współrzędne wierzchołka paraboli

małami: W zadaniu nie ma określonych żadnych współrzędnych ;x

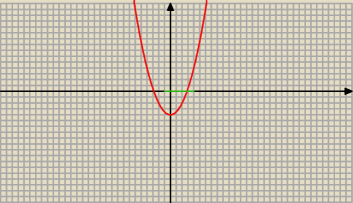
Janek191: f(x) = 0,5 x² − 4 Df = < − 1; 4 > Mamy a > 0 i p = 0 , więc y_min = f(0) = 0,5*0 − 4 = − 4 y_max = f(4) = 0,5*16 − 4 = 4

Bogdan: Przecież we wzorze paraboli są podane współrzędne wierzchołka, wystarczy odczytać.

	1
f(x) =		(x − 0)2 − 4 więc W = (0, −4)
	2