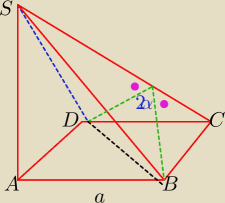
. Piotr 10: Podstawą ostrosłupa ABCDS jest kwadrat ABCD. Krawędź AS jest wysokością ostrosłupa. Odległość punktu B od krawędzi CS jest równa d, a kąt dwuścienny między ścianami BCS i CDS ma miarę 2α,

	π		π
gdzie α∊(		,		). Oblicz:
	4		2

a) odległość punktu A od krawędzi CS b) wysokość tego ostrosłupa Jak ta odległość punktu A będzie poprowadzona do krawędzi CS ?

Piotr 10: Normalnie to poprowadzić pod kątem prostym na krawędź SC z wierzchołka A ?

Mila: Tak, to jest wysokość ΔACS opuszczona z A na CS.

Piotr 10: ok, zaraz spróbuje zrobić

Piotr 10: Można prosić o pomoc? Od czego zacząć ?

Mila: Możesz obliczyc połowę przekątnej, a potem a.

Piotr 10: hmm, czy linie kolory zielonego(przerywane) są równej długości ?

Mila: Tak. Oblicz wysokość ΔBDG, G wierzchołek w kącie 2α |SD|=|SB|