.
Piotr 10: Wyznacz wszystkie wartości parametru m, m∊R, dla których równanie I Ix−4I −x I =m ma tylko
jedno rozwiązanie.
Ix−4I − x =m v Ix−4I −x = −m
Ix−4I=m+x v Ix−4I= x −m
Dalej próbowałem to podnieść obustronnie do kwadratu itd. Mi tam wychodziło zawsze m=0, na
pewno m≠−4 i m≠4 ( wyszło mi to z róźnych liczeń), lecz mam jeszcze w kluczu , m∊(4;+∞)
Tak zbytnio nie mam pomysłu, można prosić o podpowiedź ?
23 sty 20:59
bezendu:
To nie jest zadanie ze zbioru Pazdro ?
Ja bym rozbijał na przedziały ?
23 sty 21:02
Piotr 10: To zadanie z arkuszy z Pazdro
23 sty 21:04
Eta:
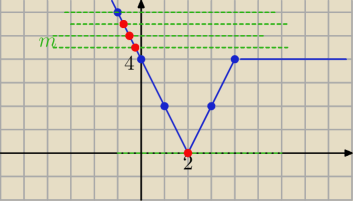
23 sty 21:06
Piotr 10: Czyli jednak narysować ten wykres ?
23 sty 21:08
Eta:
Narysuj wykres przedziałami dla x≥4 i dla x<4
23 sty 21:08
bezendu:
Czyli tak jak myślałem.
23 sty 21:12
Piotr 10: Okej, zrobione dziękuję
23 sty 21:14
Eta:
23 sty 21:15
bezendu:
Ale jest zła odpowiedź w arkuszu bo jeszcze m=0 również jedno rozwiązanie
według mnie tak: m∊{0}∪(4,∞)
23 sty 21:16
Piotr 10: W kluczu też jest m=0
23 sty 21:17
bezendu:
To widocznie źle przeczytałem.
23 sty 21:19
Marcin: Z tego co widzę, to na rysunku jest zaznaczone m=0 i (4,
∞)

23 sty 21:19

