oblicz granice funkcji matmaaa:

	x4−8x+7
lim		, gdzie x→1
	x4−4x+3

Ada: Oba wielomiany dzielą się przez (x−1).

matmaaa: ale jak to rozpisać?

Janek191: ( x⁴ − 8 x + 7 ) : ( x − 1) = x³ + x² + x − 7 −x⁴ + x³ −−−−−−−−−−− x³ − 8 x − x³ + x² −−−−−−−−−−−− x² − 8x − x² + x −−−−−−−−−− − 7 x + 7 7 x − 7 −−−−−−−− 0 czyli x⁴ − 8 x + 7 = ( x − 1)*( x³ + x² + x − 7 ) Analogicznie x⁴ − 4 x + 3 = ( x − 1)*( x³ + x² + x − 3) więc

	x3 + x2 + x − 7
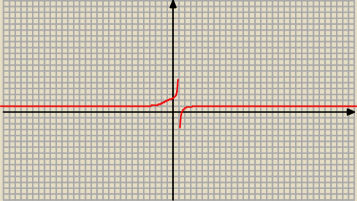
lim x→ 1−		= +∞ granica lewostronna
	x3 + x2 + x − 3

oraz

	x3 + x2 + x − 7
lim x → 1+		= − ∞ granica prawostronna
	x3 + x62 + x − 3