wykaż na podstawie definicji, że funkcja f jest malejąca w przedziale zunia: Funkcja kwadratowa f opisana jest wzorem f(x) = −0,5x² + x + a² − 4, gdzie a jest parametrem (a ∊ R) a) wykaż na podstawie definicji, że funkcja f jest malejąca w przedziale (1, +∞), dla dowolnego a ∊ R b) Wyznacz wartość parametru a, wiedząc, że różnica miejsc zerowych funkcji f wynosi 10

Ada: f jest malejąca ⇔ ∀x₁, x₂ ∊(1,+∞): x₁>x₂ ⇒f(x₁)<f(x₂) ⇔ f(x₁)−f(x₂)<0 Z:x₁>x₂

	1		1		1
f(x1)−f(x2)=−		(x1)2+x1+a2−4−(−		(x2)2+x2+a2−4)=−		[(x1)2−(x2)2]
	2		2		2

	1		−1
+x1−x2=		[(x1)2−(x2)2+2x1−2x2+1−1]=		[(x1)2+2x1+1−[(x2)2+2x2+1]]=
	2		2

−1
	[(x1+1)2−(x2+1)2]
2

Badamy znak nawiasu: x₁>x₂ z założenia ⇒ x₁+1>x₂+1, dla x>1 kwadrat rośnie, czyli (x₁+1)²>(x₂+1)² ⇔(x₁+1)²−(x₂+1)²>0 a nawias mnożymy przez liczbę ujemną więc spełnione jest: f(x₁)−f(x₂)<0

zunia: dalej nie bardzo rozumiem..

Ada: Definicji, czy przekształceń

zunia: definicji

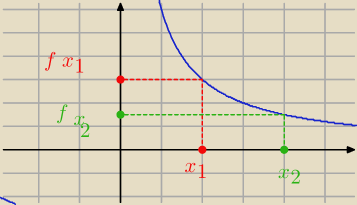
Ada: Funkcja jest malejąca jeżeli dla każdego x₁ mniejszego od x₂ wartość funkcji w x₁ jest większa od wartości w x₂. x₁, x₂ należą do badanego(zbioru.

zunia: Ooo.. teraz to widzę dzięki

zunia: a jak zrobić ten podpunkt b?

Ada: ze wzorów Viete'a

	c
x1x2=
	a'

	−b
x1+x2=
	a'

f(x)=a'x²+bx+c (x₁−x₂)²=x₁²+x₂²−2x₂x₁=(x₁+x₂)²−4x₁x₂